A Potential Simple Analogous Heat Flow System to Explore Big History's Singularity Trend
Almanac: Evolution:Trajectories of Social Evolution
Many historical systems (e.g., civilizations) demonstrate trends towards acceleration of knowledge, energy flow, and complexity. These systems are far from thermal equilibrium as they depend on great flows of energy through them to maintain their structure, similar to Dissipative Dynamics Systems (DDS). This dissipation causes entropy, but while entropy is often associated with disorder, often ordered patterns can spontaneously develop in them to facilitate entropy generation. That is, entropy gradients (and the second law of thermodynamics) might be the driver to higher complexity. In addition, optimized engineered systems that are far from equilibrium, such as removing heat from electronic chips, also follows fractal pattern formation. A major trend in Big History is the singularity trend of complexity, which has substructure where the complexity tends to increase by a factor of about 3 for every shortening (by a factor
of ⅓) period. At the same time, the energy flow tends to increase at a slightly faster rate of about 4-5 within each period. This paper develops a simple ana-logous energy flow system that may help gain insight into this Big History trend, however, it is incomplete. Research areas are identified to tighten this approach.
Keywords: energy, environment, information, logistic.
Introduction
The purpose of this paper is to propose a potential simple (‘toy’) system that demonstrates similar trends to the Big History singularity trend. This is a next step beyond the first modeling step of identifying an equation and interpretation that describes the overall growth. The current understanding is based on a remarkably simple equation, i.e., dy/dt = ky2, and its interpretation that the ‘complexity’ is proportional to the product of the current complexity (y) and the rate of learning, which itself is proportional to the previous complexity (y) (Korotayev 2005, 2020). This accumulative learning scenario leads to the prediction of a singularity since the solution to the equation is y = A/(t - T) where T is the time of the singularity as has been observed in human populations and other natural systems (Kremer 1993; Korotayev and Malkov 2016; Fomin 2020). But there are many questions that arise from this, for example: Why does there seem to be substructure (by a factor of 3)? Is there a more general equation that helps understand what happens near and after the singularity time (since the equation's assumptions will eventually break down when change becomes too rapid)? Why does energy flow scale a bit faster than the progress (LePoire and Chandrankunnel 2020)?
It is not clear that this approach to develop an analogous system will help, but others have already made important contributions concerning trends in similar systems. The work of Schneider and Kay (1994) demonstrated that the second law of thermodynamics (entropy always increases) might actually drive the trend to higher complexity, since the spontaneous pattern formations found in such far-from-equilibrium systems actually increase the rate of entropy generation. The works of Bejan (Bejan and Lorente 2011; Bejan and Zane 2012) apply some of these principles in his Constructal Theory/Law, which shows the development of many scaling laws in evolution and engineering design due to entropy generation. Ayres and Warr (2009) developed a new understanding of the central role of energy in economics and history. Niele (2005) detailed evolutionary transitions concerning energy generation and use.
Energy flow is defined as the rate of energy use, after thermal heat losses are considered, i.e., free-energy power. Chaisson (2004, 2014) identified the energy flow density as a major determinant of complexity. He showed that the energy flow per mass through various astronomical systems such as galaxies, stars and planets tends to increase. This trend was then extended to evolving life forms, humans, and technologies. But increased energy flow through a leading technology does not determine the societal complexity necessary for sustained development. For example, while a jet engine has quite a large free energy flow, it is only useful when the society maintains the infrastructure such as economics, airports, airplane manufacturing along with a demand for the service to trade and travel. Instead, the complexity of an evolving system might be better characterized by the amount of free-energy flowing through it.
However, there are many other approaches being explored concerning the role of energy in evolution. The natural tendency of complex non-living structures is to spontaneously form from a large energy flow, as described by Bejan and Lorente (2011) and Schneider and Kay (1994). For example, when the bottom of a pot of oil is slightly heated, heat flows through the oil (conduction) to be released at the top surface. As the temperature at the bottom is increased, there is a critical temperature when the oil starts macroscopic coordinated flow structures (Bénard convection cells) that efficiently transfers heated oil from the bottom in exchange for cooled oil at the surface. A similar formation of organized structure is seen when a bathtub is drained as water forms a circular motion to more efficiently drain the water. Natural systems also display these formations in the form of hurricanes, tornadoes, and water eddies. Further studies (Horowitz and England 2017) explore the dynamics of systems far-from-equilibrium to determine relationships between energy flow, reproduction rate, entropy, decay rate, and inversion ratio (fraction of ordered systems to those in equilibrium). From these studies, evolution of complex systems is compatible with the second law of thermodynamics and in fact facilitates entropy production by organizing collective structures that reduce the energy flow gradients. As Schneider and Kay stated in 1989, ‘Nature abhors a gradient’ (Schneider and Sagan 2005: 6).
Evolutionary changes in energy flow often occur when an evolving system needs to adapt to environmental conditions (Niele 2005; Jantsch 1980). These environmental conditions may be the result of the previous growth of the system to the limits of the current way of operating. New energy mechanisms or sources are then identified and explored along with a new organizational structure to mitigate the previous limits. A set of evolutionary energy mechanisms during the growth of civilization is collected in Table 1 (LePoire and Chandrankunnel 2020). The timing of these events occurs with step durations decreasing by about a factor of 3 from the immediately preceding phase. Physical analogical models for each transition were discussed previously (LePoire 2019).
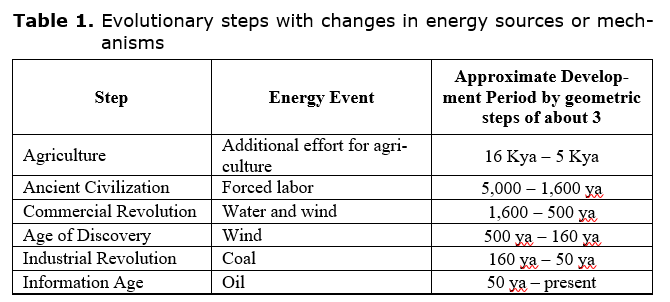
This evolution of civilization is just one of the three major evolutionary stages (life, humans, civilizations) identified by Sagan characterized by their primary information mechanisms (DNA, human brain, writing) that occurred roughly 5 billion, 5 million, and 5 thousand years ago. Each of these information stages are formed from about 6 phases where the duration decreases by a factor of three from each previous phases, leading to the overall decrease in the duration of an information stage of a factor of a thousand (LePoire 2015a, 2015b); with striking parallels with Panov's (2005, 2020) analysis, as well as Korotayev (2020) and Fomin (2020).
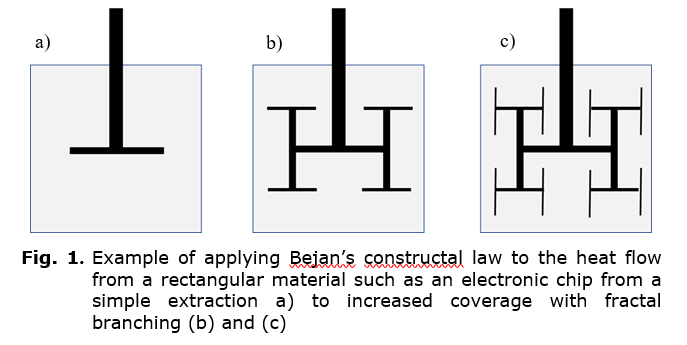
In Bejan's example of an engineered system to remove heat from a rectangular volume (Bejan 1997), such as from an electronic chip, the identified optimal solution was an ever-increasing fractal pattern on the surface, where not only the length of the conduits were fractal but also the width. This was done with very specific heat flow considerations. The pattern tended to fill the surface (see Fig. 1). The expansion onto the surface occurs through adding alternating x and y directional conduits.
Method
On a square surface, the fractal grows in alternating directions. It would be more reasonable if the scaling was consistent. This can be done by simplifying the base polygon from 4 to 3 sides, i.e., an equilateral triangle. While triangles are not found in electronic chip design, the triangular frame is often found as one of the most stable elements in civil engineering, such as bridge design. Assume that the triangle is heated from below. Other surfaces (top and sides) allow some heat to flow to the environment. The design goal is to extract as much energy as possible from surface conduits built with a given fixed amount of material. To extract the maximum amount of energy, the first extraction point would be in the center, equally from boundaries where temperature falls. The process of extracting the energy causes the center temperature to drop (see Fig. 2).
Now, if the same amount of material is available for the next stage (as with the square heat flow), the process would be repeated, splitting the material three ways but only having to traverse half the distance to the center of the 3 outside triangles (see Fig. 1c).
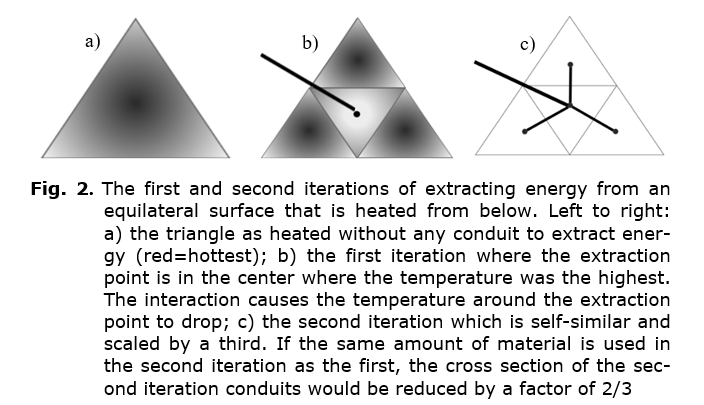
The length of the new conduits L’, is half the original, L. Since the amount of material is the same in each iteration, the material is divided into 3 for
each of the new pipes. Since the amount of material in a pipe is the product of its length (L) and cross sectional area (A), then 3 L’A’= LA, i.e., the cross sectional area is reduced by 2/3. Resistance (R) to flow in a given pipe is proportional to the length and inversely proportional to the area, i.e., L/A. This gives a flow resistance of 3/4 of the previous conduit. However, there are three pipes in parallel now feeding the main node, so the net energy extracted from the three pipes would be 3/R = 4 times the energy extracted in the original pipe. If the material is laid out at the same rate for each of the pipes compared to the original, the time for the construction is 1/3 the original time. So the second iteration takes 1/3 the time to build (with three lines going on simultaneously). The amount of energy extracted is 4 times as much, since there are 3 shorter conduits but with smaller cross sections.
This continues for the next iterations (see Fig. 3), with the energy increasing by a factor of 4, taking a third of the time, with the population of new nodes being about 3^(n-1). The total number of nodes N will approach (3^n)/2 when the number of iterations n gets large. So this model has similar scaling to what is seen (of population or complexity) in the rate of Big History transitions: N scales as 1/(t-ts); energy scales at a higher rate than N (by a factor of 4 for every factor of 3 increase in N). It is important to realize that a difference with Bejan's square model is that there are areas that are being passed over, whereas in the square geometry, all areas are being extracted.
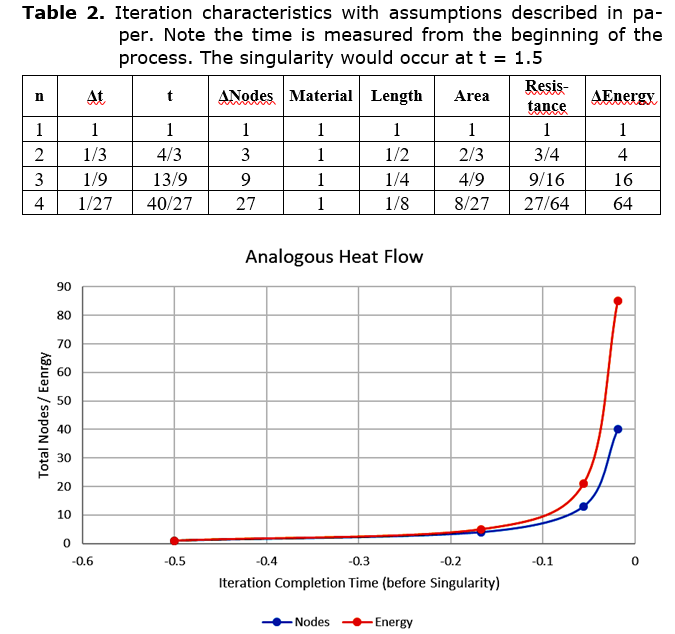
However, with each iteration the extraction becomes a bit less efficient because the boundaries are being approached. Eventually, it would be more advantageous to fill in the triangle gaps instead of branching out. For example, as the 3 triangles are explored in Fig. 1c, there is about 25 % (the central triangle) abandoned. For each iteration there is another quarter of the area being explored left abandoned. This adds up, so that the fraction of the abandoned area to the area being used for extraction scales as 4/3 ^ n. At the full extension of the exploration, this leaves quite a large fraction of energy to be extracted. For four iterations in Fig. 3b, the ratio of area abandoned to the area for extraction is about 4. While this is quite small compared to the ratio of extraction from the full extension with compared to the first single node of almost 64, there are significant resources to be utilized.
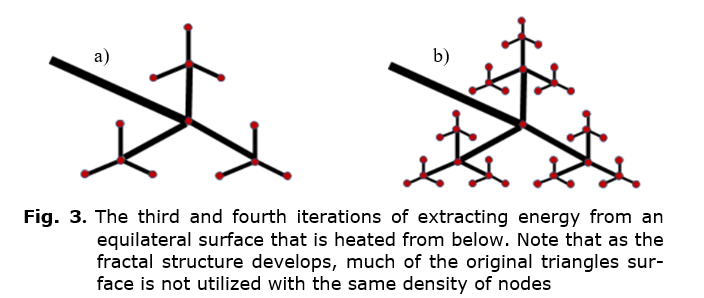
However, this is not what was expected for a truly symmetrical transition after the peak, where it was expected that the growth of complexity might grow by the same factor (3) but at a hyperbolically decelerating rate. This current triangular model would give an increase of 4/3 instead of a factor of 3. Each iteration after the peak would take about three times longer than the previous as the extraction pipes need to become increasingly longer.
Results
So to summarize the analogy of extracting energy from a triangular surface and the Big History singularity trend:
· Both are based on energy extraction from a far-from-equilibrium system.
· Both show singularity behavior with the number of nodes and population (or complexity) tends to increase inversely proportional to the time to the singularity.
· Both show substructure with stages of increasing by a factor of 3, in one third the time.
· Both show energy extraction (flow) at a rate greater than the number of nodes and population.
· Both would hit a limit where the effort to extract greater energy from additional iteration becomes marginal.
· Both seem to show ways that the trend might reverse. In the triangle system, much of the area is bypassed as the geometric trend is continued. In complex adaptive evolutionary systems, it has been shown that with environmental limits, the complexity might not reach chaotic state but instead reverse in complexity (Stone 1993).
· The reversal in the triangular case seems to show an unexpected factor in the energy geometric trend, falling from a factor of about 4 to about 4/3.
Discussion
While there are many similarities as listed above, it is unclear why this simple system would be analogous to the system of Big History. For example, why would the abstract space being explored be represented by a triangle instead of a square or higher dimensional structure? The triangle is the simplest 2-D polygon so fractal continues by splitting into three branches. However, in typical complex adaptive systems, the iterative branching continues by splitting into two different branches, that is, bifurcation. The bifurcations could be viewed as two opposing potential paths to realize a new organization for the next iteration. But clearly the exploration in bifurcations is in polar opposites. As seen in the case of fractal exploration of the square, the opposite directions occur along the x or the y directions but not both simultaneously. With a triangle, the three new branches from each node allow exploration in the plane, i.e., any point of the area being explored can be expressed as a linear combination of any two of them.
While detailed calculations of the heat flow from the fractal structure of the square were shown to be physically accurate, the detailed calculations were not done for this triangular case. The boundary conditions have not been specified in detail but it is believed to have a large heat source along the bottom with some type of flow (e.g., radiative) along the sides (not insulating or at a fixed temperature). It would be beneficial to fill this analysis gap.
It is important to notice that the structures are built up from only current considerations of optimization, not a long-term goal of designing an optimized complete system. In the triangular case this leads to exploring areas that are initially far away, where the current system has smaller impact on the extraction potential. This is similar to accumulative learning where foundations are set enabling further learning. For example, humans' symbolic expression did not start with writing but instead with vocal (and perhaps manual gesture) expressions that offered a wider range of options such as ability to learn quickly, not needing great production infrastructure, ability to quickly communicate in greater number of conditions (e.g., nighttime). Only later, after the opportunities opened by vocal language were filled, did the investment in writing offer marginal benefits.
Finally, the system reaches the point where marginal gain from further fractal expansion is limited. This seems to be the period we are entering. Each of the cumulative levels supports quite an infrastructure and opportunity for us.
However, in the rush to expand, many issues have been left unresolved. For example, the transition to agriculture from hunter-gathering allowed higher population growth but required greater effort; the transition to civilization allowed for defense and risk reduction in return for curtailed freedoms. An example of a recent unresolved issue is seen in the U.S. health care system, which developed in an industrial era with assumptions about jobs and medicine within a country context. The push was to globalize, leading to great advances in lifestyle and health, but the system of healthcare was difficult to upgrade as other competing issues required greater attention. These issues can now be seen as areas to be improved as the challenges of global cooperation become apparent.
To compare to the triangular case where potential areas are left unutilized as the main infrastructure is developed, then we should see many unresolved issues at many levels. One way to investigate this is to look at risks coming from various social levels. Table 3 outlines the occurrence of events from the personal (addiction to alcohol and drugs) through the family (divorce), group (layoffs), community (crime), and national (identity theft) levels. Identity theft is depicted as a national level problem because, while some identity theft is international in scope, most occurs from within the victim's country. Table 3 shows that life-impacting events across these various social levels affect around 5 % of the U.S. population. These events can typically cause severe life changes and stress.
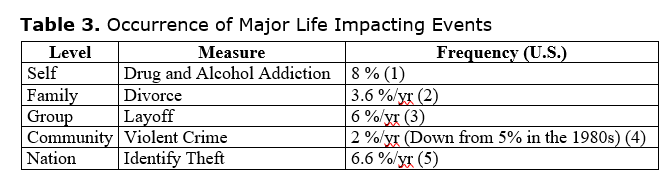
Sources: URL: http://www.aa-uk.org.uk/alcoholics-anonymous-reviews/2006/02/alcoholism-and-drug-dependence-are.html; URL: http://www.cdc.gov/nchs/fastats/divorce.htm; http://www.statcan.ca/english/freepub/75-001-XIE/10304/art-2.pdf; URL: http://www.ojp.usdoj.gov/bjs/glance/viort.htm; URL: https://www.identityforce.com/blog/identity-theft-odds-identity-theft-statistics.
While conventional responses do have a place in the reduction of the threat, alternative complementary approaches have been suggested. One alternative advocated by the late Nobel Prize winning chemist Richard Smalley (2003), soon after the 9/11 attacks, called for an international collaboration to develop energy and technology as one way to help alleviate multiple world problems. In this situation, the developed world might be seen as addressing common problems with agreed upon technological use. This is an example of an alternative approach integrating a wider systems-level view to the problem where the conventional linear approach might no longer be applicable. Developing and motivating U.S. students to pursue science and engineering fields was an important factor in this proposal, since currently about half of the students in these programs are attracted from other countries.
A systemic approach to these issues would compare and investigate the relationships of the relative risks and possible actions (Tainter 1996). This can be refined further by taking a look at the combinations of threats, vulnerabilities, and consequences. The factors leading to increased vulnerability include untested new technologies; dependence on technologies and resources; operating with limited political, economic, and public communication capacities; and complex interactions. The factors leading to a decreased threat level include more equitable distribution, toleration, transparency, trust, and opportunities. Consequences can be physical, financial, or psychological but could be mitigated through appropriate responses including planning, assessment, and forecasting potential unintended consequences.
Conclusion
A simple (‘toy’) system with heat flow on a triangle was explored as motivated by Bejan's analysis of a system on a square. The evolution of a heat extraction system on a triangular surface was seen to have many characteristics similar to the long-term singularity trend in Big History. As with all models, there are many gaps and differences. However, having one physical system to reference might provide insights for further development.
One similar property is that in their evolution with the singularity trend, many potential resources are left behind. This suggests that the inflection of this trend (since it cannot continue to an actual singularity) might be to slow down and try to resolve some of the issues that remained in the rush to develop the base infrastructure. One approach to support this was to identify risks at various social levels. The risks seem to be spread out over many levels from self to global issues.
References
Ayres R. U., and Warr B. 2009. The Economic Growth Engine: How Energy and Work Drive Material Prosperity. Cheltenham, UK: Edward Elgar Publishing.
Bejan A., and Lorente S. 2011. The Constructal Law and the Evolution of Design in Nature. Physics of Life Reviews 8: 209–240.
Bejan A., and Zane J. P. 2012. Design in Nature: How the Constructal Law Governs Evolution in Biology, Physics, Technology, and Social Organization. New York: Doubleday.
Bejan A. 1997. Constructal-Theory Network of Conducting Paths for Cooling a Heat Generating Volume. International Journal of Heat and Mass Transfer 40(4): 799-810.
Chaisson E. 2004. Complexity: An Energetics Agenda: Energy as the Motor of Evolution. Complexity 9(3): 14–21.
Chaisson E. 2014. The Natural Science Underlying Big History. The Scientific World Journal: 1–41.
Fomin A. 2020. Hyperbolic Evolution from Biosphere to Technosphere. The 21st Century Singularity and Global Futures: A Big History Perspective / Ed. by A. Korotayev, and D. LePoire, pp. 105–118. Cham: Springer.
Horowitz J. M., and England J. L. 2017. Spontaneous Fine-Tuning to Environment in Many-Species Chemical Reaction Networks. Proceedings of the National Academy of Sciences 114(29): 7565–7570.
Jantsch E. 1980. The Self-Organizing Universe: Scientific and Human Implications of the Emerging Paradigm of Evolution. Oxford, UK: Pergamon.
Korotayev A. 2005. A Compact Macromodel of World System Evolution. Journal of World-Systems Research 11(1): 79–93.
Korotayev A. 2020 The 21st Century Singularity in the Big History Perspective: A Re-Analysis. The 21st Century Singularity and Global Futures. A Big History Perspective / Ed. by A. Korotayev, and D. LePoire, pp. 19–75. Cham: Springer.
Korotayev A., and Malkov A. 2016. A Compact Mathematical Model of the World System Economic and Demographic Growth, 1 CE – 1973 CE. International Journal of Mathematical Models and Methods in Applied Sciences 10: 200–209.
Kremer M. 1993. Population Growth and Technological Change: One Million B.C. to 1990. The Quarterly Journal of Economics 108(3): 681–716.
LePoire D. J. 2015a. Interpreting ‘Big History’ as Complex Adaptive System Dynamics with Nested Logistic Transitions in Energy Flow and Organization. Emergence: Complexity & Organization 17(1): 1–16.
LePoire D. J. 2015b. Potential Nested Accelerating Returns Logistic Growth in Big History. Evolution: From Big Bang to Nanorobots / Ed. by L. E. Grinin, and A. V. Korotayev, pp. 46–60. Volgograd: ‘Uchitel’.
LePoire D. J. 2019. An Exploration of Historical Transitions with Simple Analogies and Empirical Event Rates. Journal of Big History 3(2): 1–16.
LePoire D. J., and Devezas T. 2020a. Near-term Indications and Models of a Singularity. The 21st Century Singularity and Global Futures. A Big History Perspective / Ed. by A. Korotayev, and D. LePoire, pp. 213–224. Cham: Springer.
LePoire D. J., and Chandrankunnel M. 2020b. Energy Flow Trends in Big History. The 21st Century Singularity and Global Futures. A Big History Perspective / Ed. by A. Korotayev, and D. LePoire, pp. 185–200. Cham: Springer.
Niele F. 2005. Energy: Engine of Evolution. Amsterdam and Boston: Elsevier.
Panov A. 2005. Scaling Law of the Biological Evolution and the Hypothesis of the Self-Consistent Galaxy Origin of Life. Advances in Space Research 36(2): 220–225.
Panov A. 2020. Singularity of Evolution and Post-Singular Development in the Big History Perspective. The 21st Century Singularity and Global Futures. A Big History Perspective / Ed. by A. Korotayev, and D. LePoire, pp. 439–468. Cham: Springer.
Schneider E. D., and Kay J. J. 1994. Life as a Manifestation of the Second Law of Thermodynamics. Mathl. Comput. Modelling 19(6–8): 25–48.
Schneider E. D., and Sagan D 2005. Into the Flow: Energy Flow, Thermodynamics, and Life. Chicago: University of Chicago Press.
Stone L. 1993. Period-doubling Reversals and Chaos in Simple Ecological Models. Nature Cell Biology 365: 617–620.
Tainter J. A. 1996. Complexity, Problem Solving, and Sustainable Societies. Getting Down to Earth / Ed. by R. Constanza, O. Segura, and J. Martinez-Alier, pp. 61–76. Washington, D.C.: Island Press.
