Can Humanity Escape the Earth?

Download

At the time of European discovery, the Old World, Americas and Australia had populations and technological levels that were ranked in the same order as their size. In Australia, population and technology had remained steady for thousands of years. This suggests that the size of an isolated territory limits both the population and the technology it can achieve. Since world population growth is slowing down, it could be that humanity as a whole is approaching the population limit – and hence the technological limit – that a planet the size of the earth can support. The question is whether space colonisation lies within this limit, so that humanity can escape the earth's boundaries, or whether it is beyond the limit, so that humanity will converge to a stagnant, earth-bound equilibrium. Drawing on existing models of social macrodynamics, the author concludes that earth is probably just large enough for escape to occur.

Keywords: social macrodynamics, world population, technological evolution, space colonisation.

John Marc Widdowson, Independent researcher, Bourne, Lincolnshire more

Introduction

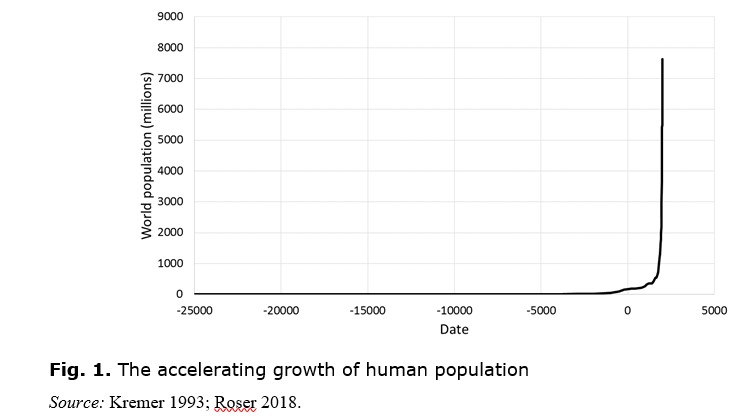
The human race has come a long way, from the stone axe to the iPhone, and, as is common knowledge, this progress has occurred at an accelerating pace. It has been accompanied by a similar acceleration in the growth of world population (see Fig. 1).

Extra-terrestrial anthropologists observing this growth from the distance of, say, Alpha Centauri might logically expect that it would continue. They would have no reason to suspect that a dynamic that has been in place for at least 30,000 years – even for several million years – would suddenly come to an end just as they happened to be watching. Continued growth would mean that the fundamental discoveries of past centuries – ocean navigation, various kinds of engine, electricity, heavier-than-air flight, radio, semiconductor chips – should be followed by equally fundamental discoveries at ever more frequent intervals – fusion power, weather control, space travel, ocean colonisation, manipulation of the human genome, matter transportation. Indeed, the only feasible way for the dramatically rising curve of Fig. 1 to continue would be for the human race to move off the small planet it currently inhabits and expand through the cosmos, where there are unimaginably large reserves of energy, raw materials and living space to sustain such explosive growth. Extra-terrestrial observers might feel secure in concluding that this is the way things are going since they would see that humans have already visited their planet's satellite and are now clambering into orbit in an ever more determined way.

However, here on earth, confidence in humanity's ability to continue expanding and progressing is little in evidence. Mainstream discourse focuses on the finiteness of the planet and the limits it presents to human ambitions. International concerns regarding climate change or exhaustion of hydrocarbons betray an assumption that humans will remain confined to their home planet and that technology will remain largely at its current level.

Such concerns and attitudes could be seen as the result of humans' perennial chronocentrism – the belief that the present is a special moment of culmination, rather than that it is an entirely typical moment blending unremarkably into the general pattern of social evolution. The early Christians believed that the day of reckoning was near, and there has barely been a time when the end of the world was not expected by at least some elements of society. The idea that civilisation can go no further has a long pedigree (Herman 1997). That people today see the world as on the brink of ecological disaster, with too many humans on the planet and dwindling resources, is to be expected as a continuation of this way of thinking, albeit that such fears have never been realised.

An alternative strand of thought, that of the ‘techno-optimists’, considers human technology as the continuation of a long process of cosmic evolution characterised by increasing complexity (Panov 2005; Kurzweil 2005). Not only does this view provide a close fit to the history of cosmic, biological and social innovation going back billions of years, but it can be linked theoretically and empirically to the population growth curve of Fig. 1 (Korotayev 2018, Appendix 1). Furthermore, it predicts, by extrapolation, an explosion of technological capability in the mid-21^st century. This has been called the ‘singularity’ after the mathematical term for the point on a graph where the function becomes infinite. It implies a capability so advanced that it must surely propel humanity into the cosmos with almost magical technologies previously known only from science fiction.

If what is coming is, say, the conversion of the asteroid belt into a Dyson sphere, followed by interstellar travel and the colonisation of the galaxy with its estimated 40 billion earth-like planets (Petigura et al. 2013), then contemporary initiatives for sustainability on earth would seem as misplaced as if the Romans had reined in their industrial activities out of concern that the people of the 21^st century would run out of firewood.

The problem is that this may not be what is coming. The idea that the historical process is, if not reaching its end, transitioning to a new regime is no longer hypothetical or imaginary. There is evidence that it has passed a point of inflection where the curve turns over (Korotayev 2018: 104). World population growth is slowing down rapidly. Fundamental innovation, notwithstanding subjective impressions, is rarer (Gordon 2016; Cowen 2010; Huebner 2005). After the promise of the Apollo programme, manned space exploration has fallen back to a desultory though exceedingly costly effort with just a handful of people in orbit at a time. Everything suggests that humanity will achieve demographic equilibrium in a century or so, and then, if technological progress does not cease altogether, it will presumably function differently, bringing improvement at the margins, not the radical transformations of the past.

The belief of techno-optimists that technological progress is natural and inevitable is contradicted by the case of Australia, whose aboriginal inhabitants were still using Mode 3 stone tools – simpler than the Mode 4 tools developed in the Old World Upper Palaeolithic – at the time they were reached by Europeans. Had the other continents sunk beneath the waves following the colonization of Australia, there is every reason to think that the human race would be in the Stone Age to this day, with no indication it might ever move beyond it. The extra-terrestrial observers from Alpha Centauri would have seen a species in technological stasis, persisting with its rudimentary material culture until it was perhaps wiped out by some cosmic catastrophe. The human race would then have come and gone on this planet without ever knowing the travails of a farming lifestyle, or knowing Newton's laws or the scale and structure of the universe.

There arises the possibility that the ongoing curtailment of the previously explosive growth of the human species is a larger example of what happened in Australia. Equilibrium has taken longer to reach and is at a higher level, but the endgame for humanity is nevertheless one of stasis and isolation within a confined region. Unless cosmic visitors arrive to connect humans to a wider galactic community, social evolution could be essentially over, and what humans know now, and what they can do, is pretty much all they will ever know or be able to do.

On the other hand, perhaps such a conclusion is premature, and the world is only witnessing a transient slow-down. Probably, the present trickle into space will turn into a flood and, just as physicists proclaimed that physics was all but complete shortly before the revolutions of relativity and quantum mechanics, perhaps discoveries around the corner are about to unleash not only major technological advances but resumed demographic expansion.

According to Grinin's concept of ‘production principles’, humanity is currently in Stage 2 (Adolescence) of a macro-technological cycle (Grinin 2012: 15–45). This is equivalent to the period before the Industrial Revolution, when new ideas were coming in but society still had a rural and traditional character, and the transformation brought about by steam power and the rise of factories lay in the future. Grinin's model suggests that it will be after 2030 or 2040 that the present ‘information-scientific’ production principle leads to a full-scale displacement of population and change in the nature of work, which is consistent with the idea of a large-scale colonisation of near earth orbit, supported by artificial intelligence and perhaps new, super-abundant power sources.

The Korotayev–Malkov–Khaltourina Model

To deal with these issues more formally, the place to start is with Korotayev, Malkov and Khaltourina's compact macromodel of demographic-technological evolution (2006a). This model, which simplifies and extends the work of earlier theorists (especially Kremer 1993), provides an exceptionally powerful and precise explanation of the curve of world population growth since around 25,000 BC, which is found to follow a hyperbolic trajectory. In its most compact form, the model can be reduced to two assumptions and a line of derivation, as follows.

The first assumption is that population N is proportional to technology T. When people lived by hunting and gathering, they inevitably lived at low densities. If there were too many people in a band, they would exhaust the resources of a district more quickly than they could move on to a new territory. If there were too many people in the world, bands attempting to move to new districts would find others already there having consumed what they had to offer. With the transition to agriculture – most likely necessitated by precisely such population pressures and resulting food shortages (Boserup 1965; Cohen 1977) – it became possible to support more people from the same territory, and the human population could satisfactorily increase.

In general, throughout history, technology has determined the carrying capacity of the land, and population has expanded to this level. This can be termed a Malthusian assumption, in that Malthus articulated clearly the way the technology of food production limits population (Malthus 1978 [1798]). In symbols, this can be written as:

Clearly, population cannot really become infinite, and thus the population growth must deviate from its hyperbolic trajectory some time before the singularity is reached. Up to about 1970, world population was exceptionally well described by a hyperbolic curve (see Fig. 2, where the line represents a fitted hyperbola and the dots represent the actual data). Korotayev et al. (2006a: 28) find that the fitted hyperbola, for the data from 500 BC, has an R² value of 99.66 per cent, i.e. the hyperbola accounts for 99.66 per cent of the variation in the data. This is a remarkable result, showing that something that might be thought to be subject to numerous vagaries and contingencies – human population growth – actually follows a very simple curve when seen on the grandest scale, and, moreover, can be explained by a very simple model.

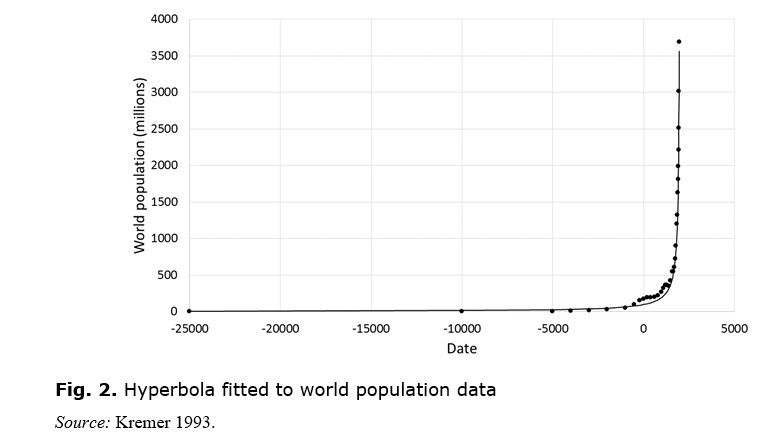
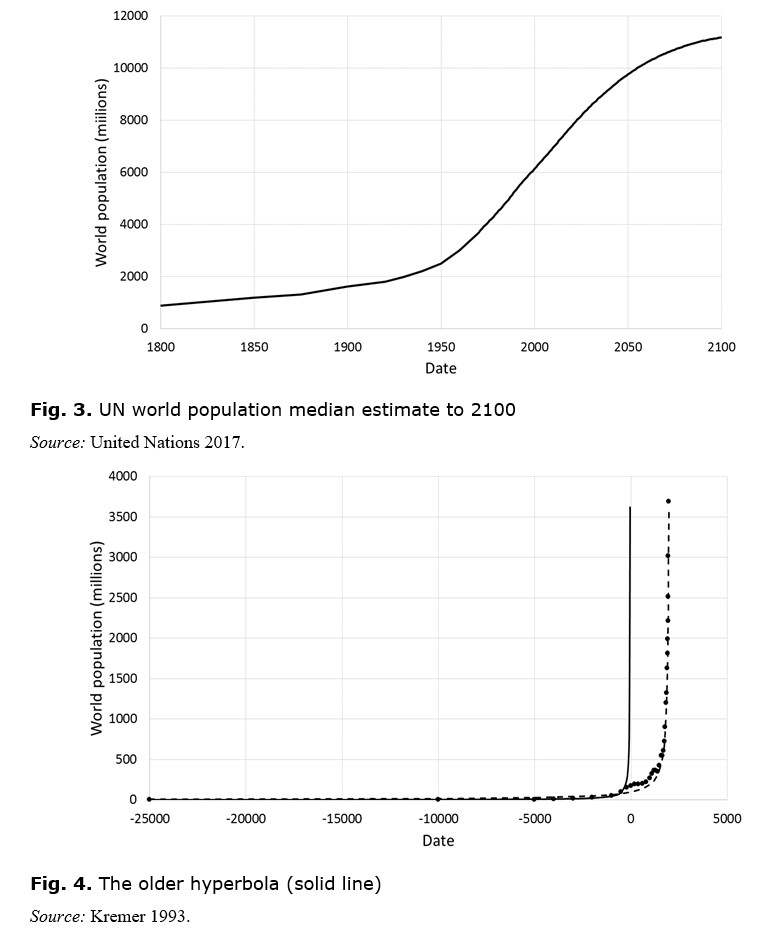
The singularity implied by the hyperbola of Fig. 2 is at c. 2026. This is the date when, from the perspective of 1970, the world population would become infinite. In fact, as Fig. 3 shows, the population growth curve has turned over and is flattening out. Far from being infinite, world population looks set to be around 8.26 billion by 2026, a little over double its value in 1970.

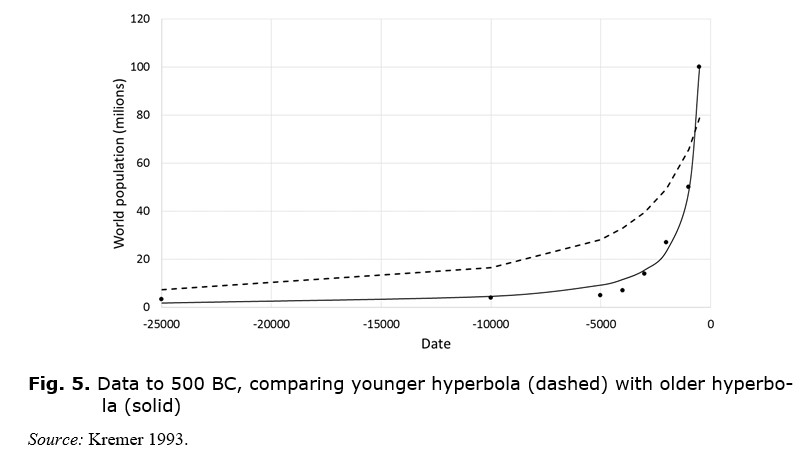
A closer look at Fig. 2 reveals that a similar flattening of the world population curve occurred for a period of about a thousand years between 500 BC and 500 AD. Prior to 500 BC, world population was following a trajectory that would have led to a singularity around 39 BC. Korotayev et al. (2006a) refer to this as the ‘older hyperbola’, contrasted with the ‘younger hyperbola’ for the trajectory up to 1970 (Korotayev et al. 2006b: 147; see Fig. 4).

 A closer view of this is in Fig. 5, showing that the older hyperbola provides a better fit to the pre-500 BC data than does the younger hyperbola.

 In fact, Korotayev et al. (2006b: 154 n. 1) suggest that the older hyperbola may itself consist of two separate hyperbolas. This is illustrated in Fig. 6, which shows the data just up to 2000 BC and compares the older hyperbola with another hyperbola calculated specifically for these data. The (even older) 2000 BC hyperbola is clearly rising faster than the ‘older hyperbola’ and has a singularity date of c. 1107 BC.

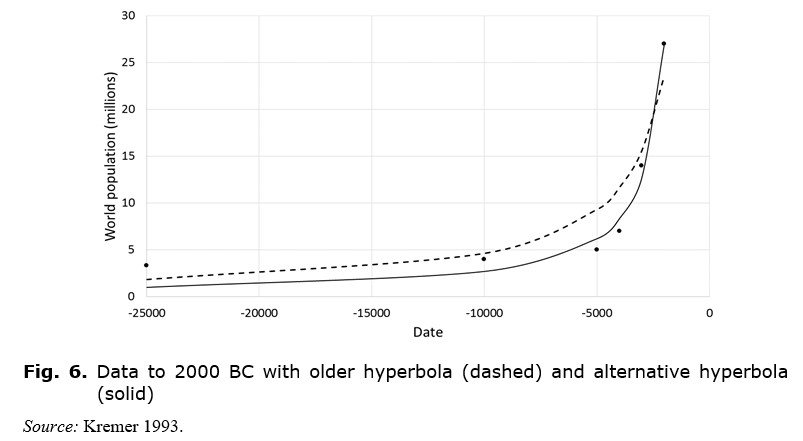
Thus, up to 500 BC, world population was rising more steeply than it was for the whole period up to 1970, and up to 2000 BC, it was rising more steeply still. Insofar as technology sets the limit to population size, this implies that technology was rising more steeply in 2000 BC than it was in 500 BC, and more steeply in 500 BC than it was by 1970. In other words, and contrary to modern intuitions, research productivity was greater earlier in history than it was later, which is to say that, while the absolute rate of invention was of course much lower than today, it was higher in terms of the rate of invention per person-year of human effort (Korotayev et al. 2006b: 158–159). Kremer (1993: 690) suggests this can be accounted for by a greater duplication of effort in a larger population.

The analysis can be extended to calculate the implied singularity date as it has evolved over world population history. This means finding the best fit hyperbola to the world population data up to the given moment. The results are plotted in Fig. 7, where the historical date is along the x-axis and the singularity date is on the y-axis; for example, the data up to AD 1 fit a hyperbola with a singularity at AD 500, which corresponds to the point (0, 500) on the graph.

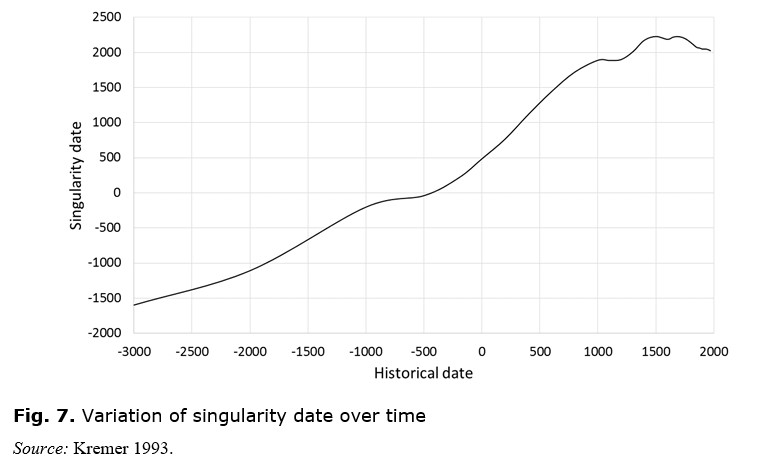
As can be seen, the singularity has mostly been moving to the right throughout history, implying that population growth has been becoming steadily less aggressive. Only occasionally, though particularly since c. 1750, has the singularity been moving to an earlier date, indicative of an acceleration of the general trend.

Although the singularity has been receding into the future, it has not usually been receding as fast as the human race has been moving towards it. For instance, in 3000 BC, the singularity date was c. 1600 BC, 1400 years in the future, whereas in 2000 BC, it was c. 1100 BC, only 900 years in the future. The singularity was 500 years nearer than before. This is illustrated in Fig. 8, which shows the time remaining to the singularity as a function of year.

In Fig. 8, when the graph is falling, population is growing vigorously and closing in on the singularity; when it is rising, the reverse is true. It can never actually reach the bottom, which would mean reaching the singularity and achieving infinite population.

Figs 7 and 8 show that, while world population growth follows an amazingly simple trajectory, it nevertheless reveals a certain amount of structure, which may shed light on historical processes.

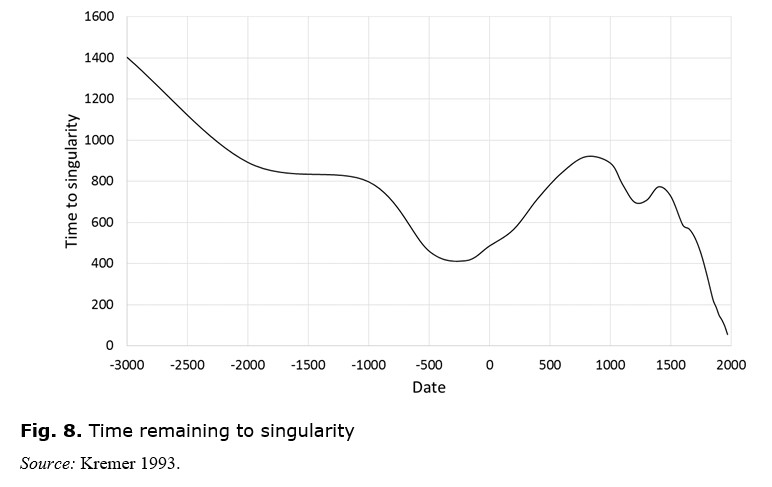
 ·   The rapid decline of the time to the singularity after 1750 seems related to the inauguration and spread of the industrial revolution, with the global integration it made possible. This turn-down began more modestly around the time of the Renaissance, which Grinin identifies as the true start of the Industrial production revolution.

·   An earlier period of falling time-to-singularity was from 3000 to 2000 BC, which can perhaps be linked to the invention and spread of bronze-working – an earlier Industrial revolution, while the fall from 1000 BC up to about 300 BC can be linked to the coming of iron – yet another industrial revolution.

·   Conversely, the fall of the time-to-singularity was arrested during the era of mature Bronze Age civilisation, in the 2^nd millennium BC, and again during the era of mature classical civilisation, from the 1^st millennium BC to the 1^st millennium AD. Given the close link between population and technology, these periods of maturity could be seen as periods of less transformative innovation. While the Bronze Age stasis saw the time-to-singularity just stop falling, the classical era and its aftermath saw the time-to-singularity actually rise, to reach a level higher even than it had been during this Bronze Age stasis. The rise in time-to-singularity only ended in the late 1^st millennium, with the ending of what were traditionally called the ‘dark ages’.

The curve in Fig. 8 can thus be divided into alternating phases of falling time-to-singularity and static / rising time-to-singularity, with the former being associated with technological revolutions (bronze, iron, industrialisation) and the latter being associated with mature hegemonic world orders. These phases each lasted about a thousand years, though this may be just an artefact of the particular window chosen for investigation, which is dictated by data availability. The initial phase, which is truncated at the beginning, may have lasted longer than a thousand years, while the other phases only approximately fit a thousand-year pattern.

The downturn of time-to-singularity that began towards the end of the 1^st millennium AD went into reverse and climbed again during the 14^th century. An obvious reason for this is the Black Death. While that is a proximate factor, it may be a symptom of a deeper explanation. Given that demography is to be understood as responding to technology – something that is not just an a priori assumption but is justified by its success in explaining demographic history – then disease should be seen as part of a nexus of causes. For example, the upturn of time-to-singularity might be understood as reflecting a failure of technological innovation to keep up with the (medical, epidemiological) challenges of an increasingly connected world. Understanding that failure, which is endogenous and sociological, may then have more useful implications for theoretical history than appealing to the exogenous natural disaster of the plague.

The recent slow-down of population growth, implying a turning away of the time-to-singularity curve from the x-axis, can now be seen as inevitable, since the x-axis, representing the unattainable singularity, is a kind of repelling boundary. Fig. 8 shows that such a repulsion has occurred before and, while it lasted a thousand years, it did not turn out to be the end of transformative technological progress – the curve would eventually turn down again, with major innovations from the windmill to electricity and nuclear power. In the same way, the present recoil should not be assumed to be a permanent end to hyperbolic growth or to technological breakthroughs. It is nevertheless clear from the above figures that the hiatus beginning now could last as much as a millennium, and science fiction technologies, like colonisation of other planets, might be long delayed.

The period of stasis need not be experienced as problematic. It might seem instead like an era of mature civilisation in largely happy equilibrium, albeit, if the previous such phases are representative, one that ends in an episode of political, economic and cultural dissolution like the ‘dark ages’ that ended the bronze and iron age world orders.

Whether the present demographic slow-down is a temporary or permanent phenomenon cannot be answered with the model presented so far. There is a need for a better understanding of what might lie behind the rises and falls of the time-to-singularity. The basic hyperbolic shape of the growth curve is driven by the Malthusian-Kuznetsian dynamics of Eqs 1 to 3. The distortions to this shape imply the existence of other factors.

An Extended Model

A more nuanced presentation of Eq. 1 above is that population growth follows a logistic trajectory, rising asymptotically towards the limiting value given by the carrying capacity. In other words, it obeys the equation:

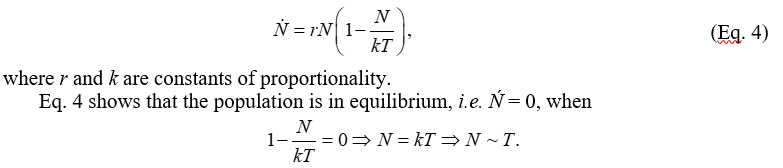
Hence, Eq. 1 follows from the normal logistic model for population growth, with the proviso that growth is rapid enough that population will usually be at its limiting value. Here, ‘rapid enough’ means that it is rapid compared to the growth of technology. It has been a reasonable assumption for most of history. Unconstrained human population growth can be very rapid, at 3 per cent a year or more (Korotayev et al. 2006b: 49) – on Pitcairn Island after settlement by the Bounty mutineers and among the early American settlers, it reached from 6 to 7 per cent (Renfrew 1984: 190; Buckminster Fuller 1969: 231) – whereas for most of history overall growth rates have been much lower, a fraction of one per cent.

Thus, population growth has a fast dynamic described by Eq. 4 and a slow dynamic described by the middle part of Eq. 3. It is the slow dynamic that matters for the long-term population growth shown in Fig. 2 and the model behind it. In effect, population is always pushing upwards and follows an envelope set by technology and the resultant carrying capacity.

By the logic of hyperbolic growth, as population approaches infinity at the point of singularity, so does the population growth rate. Hence, while the actual population growth rate has always been below what might be considered the human biological limit of 3 to 7 per cent per annum, had hyperbolic population growth continued much beyond 1970, this would have no longer been the case. It might be thought that this implies an absolute limit to how fast population can grow. Since the growth rate peaked at 2.1 per cent in 1967 (Roser 2018), the ending of hyperbolic growth could be seen as an inevitable and permanent consequence of humanity bumping up against this biological limit.

However, the human birth rate is not biologically limited and could be increased by technological means: for example, by cloning and artificial wombs. The present organic method of human reproduction might one day be seen as primitive and might be left behind, so this cannot be considered as any kind of ultimate limit.

Furthermore, the possible adoption of new reproductive technologies is not a matter of chance. The success of the Korotayev et al. model shows that, at the largest scale, there is a compelling logic to the link between technology and population growth that is insensitive to detail – Neolithic agriculture, iron metallurgy and medieval windmills all affected human capacities in particular ways but their complex idiosyncrasies somehow disappear in the powerful principle that N ~ T. Therefore, it is not necessary to consider how or why human reproductive capacities could be expanded. The millennia-attested logic shows that technology will find a way.

It follows that the present slowdown must be understood as a matter of technological underperformance rather than as a matter of physiological constraints. After all, the growth rate has not stabilised at 2.1 per cent, or at a level close to the biological maximum, but has fallen back to near 1 per cent, and looks set to fall much further, as far as zero. The physiological constraint is not the issue.

Korotayev et al. show further that the slowdown can be explained in terms of a link between ‘human development’ – in the sense of the United Nations Human Development Index (UNDP 2018) – and declining fertility. With rising standards of living, and declining child mortality, there is, in the terms of population ecology, a switch from r-strategies, involving the production of many offspring in the hope a few will survive, to K-strategies, involving the production of a few offspring that are carefully nurtured and protected (on r-and K-strategies, see Begon and Mortimer 1986). This results in fewer children and reduced population growth rates. Korotayev et al. model this in terms of female literacy, which is both a proxy for human development and a mechanism in its own right. They present a model in which literacy follows a logistic curve, moderated by income, and, as literacy approaches 100 per cent, it chokes the population growth rate to zero. They then show that this model not only has strong statistical backing but can explain the timing and extent of the post-1970 population slowdown (Korotayev et al. 2006a: 67–80).

The Korotayev et al. literacy-based model clearly describes an actual process that has caused the fall in world fertility rates over recent decades to centuries. The link between female literacy and reduced fertility has strong support from statistics, ethnography and everyday observation. There is nevertheless scope for an alternative, abstract and generic treatment that subsumes the issue of literacy. Literacy could be seen as applicable largely to the particular historical situation of the industrialising world, and less suited for explaining the earlier ups and downs illustrated in Fig. 8. As a proxy for human development, the literacy rate may also be losing its effectiveness as literacy reaches saturation, while, even in the developed world, where literacy exceeds 99 per cent, poverty, inequality, healthcare inadequacy and other negative contributors to the Human Development Index have by no means been eliminated. Nor does the literacy-based model allow for future technological breakthroughs that will decouple human fertility from the lives and experiences of women per se, thereby possibly shifting humanity back onto a hyperbolic growth trajectory.

Australia presents a situation where population growth had reached a plateau without any literacy whatsoever. It would be desirable to have a generic model, like the compact Malthusian-Kuznetsian model, where technological detail is smeared out and seen to be subservient to some strong abstract constraint that is as applicable to Stone Age Australia and to classical civilisation as it is to the industrialising world. The literacy model would then be a specific example of how such a constraint manifests itself, just as, say, the discovery of agriculture was a specific manifestation of the powerful principle that technology growth rate is proportional to population times technology (see Eq. 2).

In Eq. 1 of the compact macromodel described above, population size is set proportional to technology as the determinant of carrying capacity. Yet in the justification of this equation, it was observed that the move say from foraging to farming led to an increase not in population per se but in the density of population. If the model refers to a fixed area, such as the whole world, then this distinction does not matter. Population is just proportional to population density, and the one can be substituted for the other. However, if the aim is to compare different land masses, then it is important to remember that it is population density, rather than population, that is proportional to technology.

Suppose there are two islands (i.e., perfectly isolated landmasses) that have the same technology, with one island having a larger area. Assume also that the islands have the same ecology. This can be assumed without loss of generality so long as the term ‘area’ is understood to mean not necessarily physical area but some kind of ‘effective area’ that takes into account ecological variation. Since the islands have the same technology, they will have the same population density – on each island, a land parcel of given size will support the same number of people. Therefore the island with the larger total area will have the larger population.

The larger population of the large island is not without consequence since, according to the Kuznetsian assumption, it implies a faster rate of technological growth. Hence, technology, population density and population would all be expected to grow faster on the larger island. If the two islands start with the same technology, their technologies will be at different levels after some time has elapsed.

An important point is that the innovation rate, hence the technological growth rate, depends not on local population density but on the overall population of the island. This is because innovations can occur anywhere on the island and then diffuse throughout (see Korotayev et al. 2006a: 30, who discuss the reasonableness (and success) of this assumption in connection with the world as a whole). Hence, the second assumption of the original macromodel is unchanged.

The model thus becomes, using A for area, and with no change to the second equation:

This shows that the effort required to achieve a given technological level, from a fixed starting point, is independent of the area. Roughly speaking, the effort required to achieve a certain technology may be 1,000 person-years, and it does not matter whether this is 100 people working for ten years or ten people working for 100 years. The smaller population takes longer to get there, but there is nothing to prevent it from doing so, and it requires only the same total expenditure of human effort. Implicitly, if the other continents had sunk beneath the waves after the colonisation of Australia, the human race would have still achieved electricity, spaceflight and the iPhone. It would just have taken a lot longer.

Therefore, with the analysis so far, the relative lack of development of Australia compared to the Old World would be understood not as stagnation but merely as the result of a much slower development. When a snapshot was taken in the early modern era, the largest region, the Old World, had progressed the furthest, the smaller but still substantial New World had progressed less far, and the very small Australia had progressed hardly at all.

This explanation (which is to be challenged and refined below) is essentially the one proposed by Kremer (1993: 708–712). Kremer's explanation has two problems.

1. The resulting prediction for the population density of the Americas is out by an order of magnitude (0.0564 persons per square kilometre versus 0.36 in actuality). Since the model has two free parameters and four data points (Old World, Americas, Australia, Tasmania), this level of disagreement is not easily forgivable. That said, Kremer deals only in physical areas and does not model the issue of ecological equivalency, so it might be possible to get a better fit by taking that into account – it would require the Americas to have a higher proportion of habitable area than the Old World.

2. The more serious problem is that the model is extremely sensitive to land area. This is illustrated in Fig. 9, which shows Kremer's curve for the relationship between population density and land area. The curve barely moves for land areas below about 70 million square kilometres, then shoots to infinity for a land area of 84.51, just above the Old World land area of 83.98. The implication is that, if the Old World had been only slightly bigger, it would by now have attained infinite population density, or in reality transitioned to some other trajectory before reaching the singularity, but in that case a single model could not explain the differential outcomes anyway.

Area and Equilibrium

The idea that Australia's lower technological level, when reached by Europeans, should be explained only in terms of developing more slowly is therefore unsatisfactory. The combination of incorrect prediction and reliance on very special circumstances, in terms of the Old World's land area, makes such a model implausible and it cannot be rescued by different parameter choices.

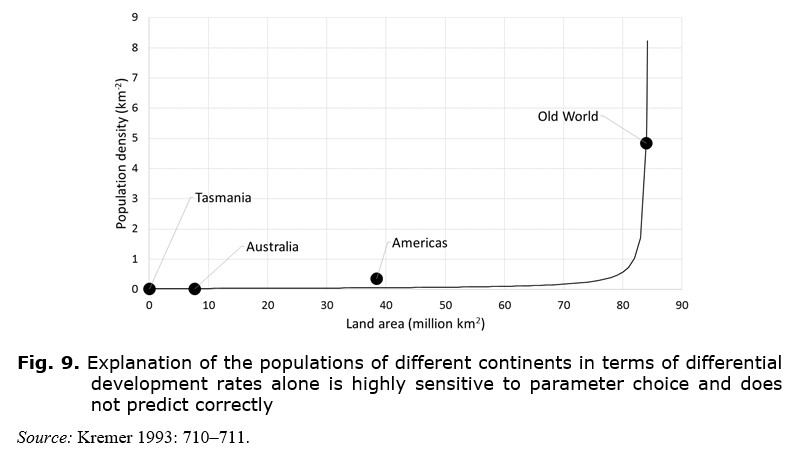
The straightforward way to resolve this is to abandon the assumption that Australia was continuing to develop just at a slower rate. Instead, Australia should be seen as having reached equilibrium and as no longer advancing technologically. This is in keeping with the subjective impression created by a technology that had not advanced beyond the Palaeolithic, achieved 30,000 or more years earlier. The completed development process of Australia (and of Tasmania) could not then be meaningfully compared with the still continuing development processes of the Americas and the Old World, and any attempt to do so would fail to find a fit, just as Fig. 9 shows.

Crucially, the lack of development in Australia did not result from a lack of dynamism, creativity or even of the trickle of ideas from the rest of the world. There was continual change in culture, in economic networks and activities, and even in specific techniques and artefacts (Hiscock 2008; Butlin 1993: 55). There were incipient forms of agriculture, and apparent experiments with more intensive cultivation that later died out (Flood 1983: 219–232; Dunbar 1995: 49). Nor was Australia truly isolated, but trade and the transmission of material culture occurred via the Cape York Peninsula (Flood 1983: 222–223).

The fact remains that there was no overall upward movement – Australians did not adopt the bow and arrow, for example – and this is best understood as due to a lack of sufficient critical mass to sustain or – to adopt a Boserupian perspective (Boserup 1965) – impel technological progress. While not completely cut-off, Australia was sufficiently disconnected from the rest of the world that it did not participate in the broader technological-demographic dynamic until the European era of discovery. It had its own dynamic, which was capped by its limited geographical size.

That this interpretation makes sense is shown not only by the way technologies could reach Australia yet fail to be adopted, but more forcefully by the example of Tasmania, where technology was even more rudimentary than in Australia (Diamond 1997: 16). The Tasmanians lost much of the technology they brought from the Australian mainland. This is to be expected if land area constrains not just the rate of technological growth but the maximum level of technology that can be achieved. After Tasmania was settled, those technologies that exceeded the limit set by Tasmania's size had to be shed.

What is more, there is a theoretical problem with the earlier idea that, on a smaller island, technology can still grow without limit, just at a slower rate. This is that, when the large and small islands have the same technology, and therefore the same population density, the small island has a smaller population. In other words, the small island is able to sustain a given technology with fewer people than on the large island. The following will explain why this is a problem.

For concreteness, suppose the technology is the iPhone. If Steve Jobs had been parachuted into an isolated Amazon village of, say, 100 people, he would not have been able to produce the iPhone even with all his expertise. The iPhone can only exist in a globally connected world that provides all the countless technologies and activities that go into making an iPhone a meaningful device and furthermore that provides one billion purchasers to make it commercially viable. An iPhone requires computer chips, touchscreens, operating systems, apps, cellular networks, billing systems and so on. Each of these requires other cascading technologies, going back for example to the people who mine and refine the metal ores that go into the phone enclosure and the microwave transmission masts. There are simply not enough people in an Amazonian village to supply the effort. It is not acceptable for this effort to be spread over thousands or millions of years, as implied by Eq. 13, where only the total effort is important not its distribution through time. This would imply thousands of years to build a chip manufacturing machine, then thousands more years before the chips were assembled into the iPhone, then thousands more years before some software was developed for it, and so on. It is not even hypothetically possible, as it would require someone at the start to map out the whole project and define it for millennia to come, and all this time the villagers would still have to be feeding and clothing themselves, raising their children, maintaining their huts, and so on. Nor is it just a case of building the phone. To make it a useful technology, in the here and now there must be people who will maintain the infrastructure and create content. Finally, with a market of only 100 people, the unit cost of the iPhones would be stupendous and completely unaffordable.

Therefore, the implication in the model of Eqs 2 and 5, or in Kremer's analysis, that, given enough time, any technology, however sophisticated, can be reached on any isolated island, however small, is completely unrealistic. Not just for the iPhone but for any technology, there must be a limiting population size below which the technology is not viable. In short, not only does technology determine the population but population determines what technology can exist. There is an inexorable link between population size and technological inventory (Turchin et al. 2018).

A technology is not just a gadget or gizmo. It is an organising principle structuring human activity. It is an open dissipative structure (in the sense of Dyke 1988: 114), like a vortex in a stream, existing not as a static object but as a persistent pattern within a flow of matter and energy. It is processual (see Fig. 10).

Fig. 10 is a more abstract justification of the point that a technology requires a minimum supporting population. It is dynamic and requires a throughput. It receives matter and energy from producers and transmits the transformed matter and energy to consumers, while dissipating a certain amount in the process. The whole system needs to be in place continuously and simultaneously, and it is closed and connected, since producers are also consumers. There can be no long-term imbalance. Consumers are as important as producers because, without consumers, there will soon be no producers.

Speed and Extent of Expansion

In the analysis above, a region is the zone containing a fully mixed, interacting population. It now needs to be considered that the ability to interact depends on technology. This is because improved transport and communications links are one of the accompaniments of technological progress, so that the region of interaction expands.

Let us consider Fig. 14. The connected region has diameter (linear size) L_c, while its area and population are A_c and N_c respectively. The region exists within an isolated island of area A and population N. Technology is assumed to diffuse in slower time than the interactions that define a connected region. That is to say, interactions are synchronous – people have to be present and interacting in real time, which means at least on sub-lifespan timescales, and the interaction is two-way – but technology diffusion is asynchronous – inventions can spread over the course of generations, and there is no necessary requirement for a return flow. Thus, T is the same throughout the island.

Escaping the Earth

According to the model presented above, the question ‘Can humanity escape the earth?’ is the same as asking whether the exceptionally low g of the interplanetary environment results in a   that exceeds the T_max of a planet the size of the earth.

In fact, it is possible that humanity's next direction of expansion will not be into space but, say, into the oceans, a large and still vastly underutilised part of the planet. In this case, humans could expand into the oceans and there gain the additional critical mass necessary for the foray into space. However, plans to colonize the oceans seem less well-advanced than those to explore space, perhaps related to the fact that the oceans present pressure differentials of thousands of atmospheres compared to the one atmosphere differential of outer space. The focus of this paper will therefore remain on the issue of space colonization.

How can such a question be answered? The approach here will use the following chain of logic:

1. Note that humanity's energy production, like population and technology, has been growing more slowly and veering towards a steady state as human progress begins to feel the limitations of the earth's size.

2. It is possible to calculate the increase in the global energy budget between now and when growth ceases.

3. This additional energy can then be compared with the amount of energy needed to establish a significant presence in space.

4. If the energy required for initial space colonization is within the extra energy expected to be available, it can be assumed that space colonisation is feasible and will go ahead.

5. Once the initial hurdle has been overcome, the project will become self-sustaining – using abundant solar power and weightless conditions to manufacture goods more cheaply than can be done on earth for example – and it can therefore be assumed expansion will continue in the new environment; it will then be possible to say humanity has escaped the earth.

To anticipate the conclusion, the finding is that the energy required is within the energy increment, though not so overwhelmingly, so the answer to the question is a tentative ‘yes’.

An author writing in the 1970s drew attention to accelerating progress in the area of energy supply in terms of the ‘ever-increasing frequency of discoveries’: fire, 50,000 years ago; then 45,000 years to water power; 3,500 years to wind power; 300 years to steam power; 100 years to the internal combustion engine; 40 years to nuclear power (Stent 1978: 28). However, since then the curve of progress has turned over and begun to decelerate. 70 years have now gone by since the discovery of nuclear power and, though ‘renewables’ like wind and solar have found a niche in the energy supply, there has been no really dramatic advance in human power generation capabilities. Indeed, nuclear is struggling to make way against environmentalist and geopolitical objections.

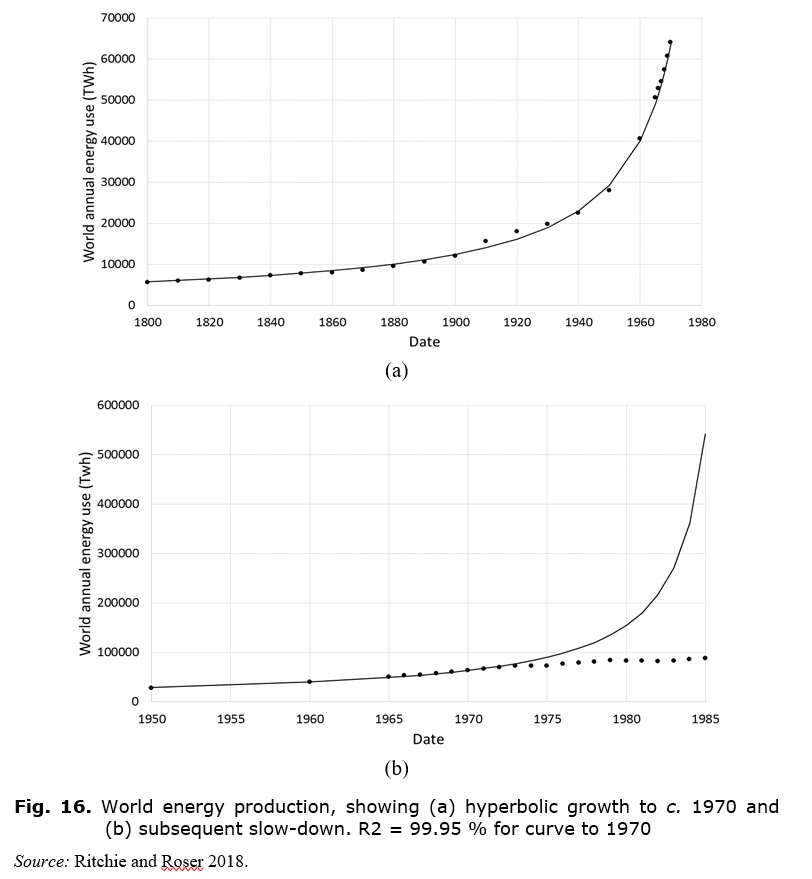
Fig. 16a shows the acceleration of world energy production from 1800 to 1970. It closely approximates a hyperbolic curve. Fig. 16b projects this curve forward to 1985, comparing it with the actual data for 1950 to 1985. The deceleration is plain to see.

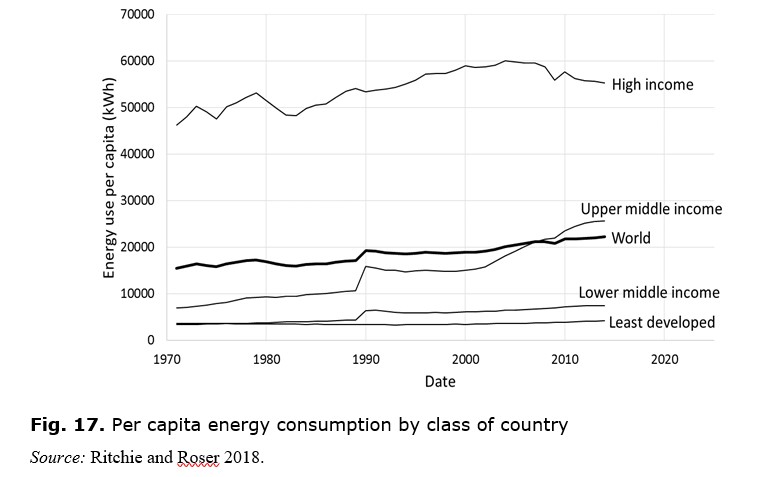
It might be expected that energy production would be quad-hyperbolic rather than hyperbolic since, as Buckminster Fuller indicated with his concept of ‘energy slaves’, per capita energy use has been increasing. The combination of increasing population and increasing use per person might be expected to produce a double acceleration. However, energy use is also subject to what Buckminster Fuller calls the principle of ‘ephemeralization’, i.e. ‘doing more with less’ (Buckminster Fuller 1969: 212–214). The modern smartphone is not only vastly more capable than the portable phones of c. 1990, but also much smaller and less demanding in materials. Thanks to ephemeralization, per capita energy use has grown less than hyperbolically and has not redoubled the hyperbolic trend of total energy use. Indeed, in the high income countries, per capita energy use has declined recently, while in the world as a whole it has climbed very slowly, despite the dramatic increase in highly populous China (see Fig. 17). Nor should it be assumed that the lower income countries will all come up to the level of the high income countries given (1) that the world is tending towards stagnation and (2) that the Pareto principle implies there will always be a distribution of incomes with few high ones and many low ones.

For the purposes of this paper, the requirement for humanity to be considered on its way to escaping the earth will be taken to be that there should be at least 10 million people living and working in space by 2040. This may seem a daunting requirement and, insofar as it does seem daunting, that illustrates the seriousness of the problem. Humanity's window for breaking out of earth's gravitational potential well is closing as population growth and technological progress approach their logistic limit. If space colonization proves a step too far now, then it will remain a step too far, and humanity will grow old on this planet at its current technological level.

The date of 2040 corresponds with Grinin's (2012) estimates for transition to Stage 3 of the present production principle, which will involve a major change in how and where people work – just as the industrialization of space would imply. The ambition of having ‘millions of people living and working in space’ also accords with the mission statement of Jeff Bezos's Blue Origin space company, where this is viewed as an active and current project, not some far future dream (Blue Origin 2018). As for the figure of 10 million, this represents the population of a small country and can be considered a demonstration that humanity truly has arrived in space.

To estimate the increment in global annual energy supply by 2040 is a simple matter. Fig. 17 indicates that per capita energy consumption will not exceed 30 MWh by then, so this can be taken as an upper limit (optimistic assumptions are appropriate, since the aim is to prove that escape from earth is at least feasible). Meanwhile, the world population of 2040, by United Nations estimates, will be about 9 billion (United Nations 2017). Thus, energy use in 2040 will be about 270,000 TWh. This compares with a current annual energy use of 153,596 TWh (Ritchie and Roser 2018), implying an increment of about 120,000 TWh, which is about 80 per cent.

To estimate the energy cost of placing and supporting 10 million people in space, it is easiest to work in terms of monetary costs. This can give an order of magnitude estimate, which is all that is needed here – (1) if the cost is an order of magnitude or more smaller than the calculated energy increment, space colonization will be easy; (2) if it is an order of magnitude or more greater, then it is impossible; (3) if it is the same order of magnitude, it is feasible but not an inevitability.

The cost of energy, assuming the cheapest (fossil fuel) sources, is about US$ 150 per MWh. The global annual energy consumption of 150,000 TWh therefore represents a cost of US$ 22.5 trillion USD. This is about a quarter of global GDP of US$ 80 trillion. Hence, on the grandest scale, about a quarter of global expenditure corresponds to energy use. This can be used to convert between energy and money. For example, the total cost of the International Space Station (ISS) is estimated to be US$ 150 billion (Wikipedia 2018). This would be taken to correspond to a total energy input, direct or indirect, worth 0.25 x 150 billion = US$ 37.5 billion, which corresponds to energy of 250 TWh (US$ 37.5 billion divided by US$ 150 per MWh).

According to this argument, the estimated increment of 120,000 TWh can be converted into an equivalent monetary amount of US$ 70 trillion (4 x US$ 150 per MWh x 120,000 TWh, rounded off to avoid spurious precision). This is the available budget.

The costs to be considered will be (1) the amortised cost of providing orbital accommodation for 10 million people plus working facilities, and (2) the annual cost of maintaining this population, for example providing food, oxygen, trips home, materials, station-keeping propellant, and ground-based infrastructure.

The cost of a passenger jet carrying about 1,000 people is around US$ 100 million (e.g., at the high end, an Airbus A380 with about 850 passengers has a list price of US$ 445.6 million [Airbus 2018]) implying a cost per passenger capacity of US$ 0.1 million. The cost of the ISS carrying 3–6 people is US$ 150 billion implying a cost per crewmember capacity of US$ 30 billion, 300,000 times as great. The cost per crewmember capacity of a large industrial space station will be somewhere between these extremes, surely closer to the airliner, enjoying returns to scale, than to the ISS, which is a small-scale experimental facility. As a reasonably conservative estimate, the cost will be assumed to be hundred times that of the commercial airliner. 10 times as much is surely too little, bearing in mind that the space station not only has to be built and then operate under more testing conditions but also, unlike a jet airliner, has to include living quarters and workspace for the crew. 1,000 times as much, implying the equivalent of a whole airliner per person, is possibly too much. Thus, the cost per crewmember will be taken to be US$ 10 million. The cost of accommodating 10 million people in space will then be US$ 100 trillion. This will be amortised over a period of 20 years centred around 2040, implying an annual capital cost of US$ 5 trillion.

For the operating cost, that of the ISS will be used as a guide. This is about US$ 3–4 billion per year for the United States (NASA 2014). Including the expenditure of other countries contributing to the ISS (primarily the Russian Federation) will bring the cost to US$ 5–10 billion per year. It will be assumed that this expenditure, which currently supports just 3–6 people in space, will be sufficient to support an airliner-sized module containing 1,000 crew members. This is on the basis that a 1,000-person crew is a realistic size of module (100 would not be cost-effective; 10,000 would be too cumbersome, at least for humanity's first attempts at space colonization), and that through efficiency savings such a module can be maintained with the same effort currently devoted to the world's existing, albeit much smaller, space station. With US$ 5 billion per 1,000-person module, the operating cost for 10 million people would be US$ 50 trillion per year. Thus, the operating cost greatly outweighs the amortised capital cost.

The total annual cost of a space colony of 10 million people is thus estimated to be US$ 55 trillion per year. This is to be compared with the equivalent US$ 70 trillion budget calculated from the increment in energy supply. Clearly, these are of the same order of magnitude. The conclusion would be that space colonization, i.e. pushing into the low-g environment of earth orbit, is just about feasible within the T_max that seems to be emerging as the limit of earthbound development. However, the margin involved is by no means so comfortable that such an outcome appears as inevitable.

Is the estimate reliable and how might one revise it in a direction more favourable to the likelihood of space colonization? Any revision is unlikely to involve the ‘budget increment’, which is determined by well-established constraints on world population and per capita energy availability. This increment is also consistent with estimates of the growth in world GDP arrived at by other means (PricewaterhouseCoopers 2017: 36). It would be possible to increase the size of the increment by pushing the deadline for space colonization out from 2040, when world population will be even larger. This could double or possibly treble the estimated increment, though it comes into conflict with Grinin's estimate of the timing of the technological transition. Alternatively, the cost of space colonization could be reduced by assuming lower costs than those above. The different assumptions should be focused on operating cost rather than capital cost, which emerges as insignificant from an annualized perspective. Specifically, it would need to be assumed that a population of at least 10,000 could be maintained in orbit for the same level of expenditure as currently maintains the handful of crew on the ISS. Such dramatic savings are certainly a feature of technological progress but it might seem optimistic to expect them for the earliest phases of humanity's expansion into orbit.

In fact, the present author is confident that human destiny does lie off the earth and eventually beyond the solar system. This is because of a belief that God would not have created this vast universe with the intention that humanity should remain confined to one tiny planet. Nevertheless, like any good puzzle setter, God has made the challenge not impossible but difficult enough to be worthwhile. It must nevertheless be admitted, on the basis of the foregoing, that a pessimist would have good reason to cast doubt on such a conclusion, and the view of many people that large-scale space colonization will never occur could turn out to be correct. The pessimist is justified because (1) the task is beyond present human capacities (or it would already have been done) and (2) the empirical and theoretical arguments given above indicate that those capacities are capped by the size of the earth and will not increase beyond twice their present value.

Even if a substantive move into space proves to be beyond the T_max of an earth-sized planet, there is a loophole, meaning it will still be possible for small groups to escape sporadically.

Consider that Australia was settled from Eurasia, and that the first inhabitants must have made at least one sea voyage out of sight of land in order to get there. Suppose then that, after Australia was occupied, humanity had been wiped out by some cataclysm on all the other continents. Although development within Australia would still have come to an end at its boundaries, and although this would be at a level below that necessary for regular travel to other continents, nevertheless it could be expected that, from time to time, reverse sea voyages would have been made from Australia to Eurasia. These voyages of occasional explorers would be enough to re-seed the World Island, where development could then proceed much further than it did in Australia, eventually leading to the world of today.

In a similar way, occasional space explorers could in future travel away from earth to seed other parts of the solar system, or perhaps establish self-sustaining settlements in earth orbit. Provided these new environments have an effective A that is greater than that of earth, they could eventually reach a technological level sufficient to incorporate the earth into a space-going civilization that it was unable to create on its own.

Conclusion

This paper is based on the works of Korotayev et al. (2006a, 2006b), which demonstrated the power of compact macromodels of the world system. It has taken the work forward by suggesting that the effect of literacy / human development on fertility is a specific mechanism instantiating a more general limitation on demographic growth and technological progress. The extended model adds just one variable, that of area, to the base variables of the Korotayev et al. model, namely population and technology. It then proposes that a given technology requires a minimum population to support it, and, insofar as this minimum tends to increase faster with technology growth than does the population that the technology supports, this implies there is a maximum technological level and population size for a given area within which growth is taking place. Area itself depends on technology because technology affects transport and communication costs. If a population finds itself surrounded by an environment – whether the ocean or interplanetary space – that it is unable to expand into with its existing technology, it becomes trapped. This way of seeing things explains the stagnation of ancient Australia and the emerging stagnation of the whole earth. It also explains the temporary slowing down of social evolution in various historical periods. Given this background, it is calculated that the requirements for a meaningful level of space colonization are only just within the expected increase in human capacities before a stagnant equilibrium is achieved some time in the next century. While it is therefore feasible that humanity will avoid the fate of being trapped on earth through not having the critical mass necessary to progress beyond it – instead escaping through a closing gap, like Indiana Jones slipping under a falling portcullis in the cave of doom – this is by no means a certainty.

Some might well argue that these conclusions are wrong. Much contemporary discourse is based on an assumption that the earth is the only planet humanity will ever know. Indeed, many people seem to think that space colonization is a science fiction concept only and cannot happen in reality – the unsuitability of the conditions for human life on other planets is often cited (e.g., Bharmal 2018; Creighton 2018). Alternatively, there is an impression that technological progress is unlimited and relies only on the accumulation of human creativity.

Against such objections, which are based more on supposition than any kind of theoretical or empirical support, certain points need to be made. First, the success of the Korotayev et al. theory in explaining human population history since the Upper Palaeolithic provides strong evidence that the relationship between population and technology is robust and correct. Second, the extraordinary achievements of the human race in transition from the stone axe to the iPhone, involving technologies that would seem magical to earlier generations, show it is foolhardy to make claims about what can or cannot be achieved in future, purely on the basis of current knowledge. Third, the example of Australia shows that progress is not inevitable and, with the additional examples of Tasmania and the Americas, that it is related to the size of the collected landmass. Fourth, the undisputable slowing of world population growth provides strong evidence that humanity is coming up against some limit imposed by the finite size of the earth, which implies a very real possibility of permanent techno-demographic stagnation. In short, the question addressed by this paper is non-trivial, and the theory used to resolve it is firmly rooted in evidence drawn from some 30,000 years of human experience.

References

37 Property Group. 2016. Habitable Land Mass. URL: http://37propertygroup.com.au/real-estate/population-density. [Date accessed: 27.12.2018].

Airbus. 2018. Commercial List Prices. URL: https://www.airbus.com/newsroom/press-releases/en/2018/01/airbus-2018-price-list-press-release.html. [Date accessed: 20.12.2018].

Barnett, W. 2003. Dimensions and Economics: Some Problems. Quarterly Journal of Austrian Economics 6 (3): 27–46.

Begon, M., and Mortimer, M. 1986. Population Ecology: A Unified Study of Animals and Plants. Oxford: Blackwell Scientific Publications.

Bharmal, Z. 2018. The Case Against Mars Colonisation. The Guardian. 28 August. URL: https://www.theguardian.com/science/blog/2018/aug/28/the-case-against-mars-colonisation. [Date accessed: 27.12.2018].

Blue Origin. 2018. We are of Blue Origin and This is Just the Beginning. URL: https://www.blueorigin.com. [Date accessed: 27.12.2018].

Boserup, E. 1965. The Conditions of Agricultural Growth: The Economics of Agrarian Change under Population Pressure. London: George Allen and Unwin.

Buckminster, Fuller R. 1969. Utopia or Oblivion: The Prospects for Humanity. Harmondsworth: Penguin.

Butlin, N. G. 1993. Economics and the Dreamtime: A Hypothetical History. Cambridge: University Press.

Cameron, R. 1992. A Concise Economic History of the World: From Palaeolithic Times to the Present. Oxford: University Press.

Cohen, M. N. 1977. The Food Crisis in Prehistory. New Haven – London: Yale University Press.

Cowen, T. 2010. The Great Stagnation: How America Ate All The Low-Hanging Fruit of Modern History, Got Sick, and Will (Eventually) Feel Better. New York: Dutton.

Creighton, J. 2018. Neil deGrasse Tyson Says Humans Will Never Colonize Mars. URL: https://futurism.com/neil-degrasse-tyson-humans-colonize-mars. [Date accessed: 27.12.2018].

Diamond, J. 1997. Guns, Germs and Steel: A Short History of Everybody for the Last 13,000 Years. London: Jonathan Cape.

Dougherty, J. E., and Pfaltzgraff, Jr. R. L. 1981. Contending Theories of International Relations: A Comprehensive Survey. New York: Harper and Row.

Dunbar, R. 1995. The Trouble with Science. London: Faber & Faber.

Dyke, C. 1988. The Evolutionary Dynamics of Complex Systems: A Study in Biosocial Complexity. Oxford: Oxford University Press.

Flood, J. 1983. Archaeology of the Dreamtime: The Story of Aboriginal Australia and Its People. London: Collins.

Gordon, R. J. 2016. The Rise and Fall of American Growth: The U.S. Standard of Living since the Civil War. Princeton, NJ: University Press.

Grigg, D. B. 1975. The World's Agricultural Labour Force 1800–1970. Geography 60 (3): 194–202.

Grinin, L. E. 2012. Macrohistory and Globalization. Volgograd: ‘Uchitel’ Publishing House.

Heaton, H. 1948. Economic History of Europe. New York: Harper and Row.

Herman, A. L. 1997. The Idea of Decline in Western History. New York: The Free Press.

Hiscock, P. 2008. Archaeology of Ancient Australia. Abingdon: Routledge.

Huebner, J. 2005. A Possible Declining Trend for Worldwide Innovation. Technological Forecasting & Social Change 72: 980–986.

Kennedy, P. 1989. The Rise and Fall of the Great Powers: Economic Change and Military Conflict from 1500 to 2000. London: Fontana Press.

Kim, M. 2015. Dimensional Analysis of Production and Utility Functions in Economics. Munich Personal RePEc Archive. Paper No. 61147. URL: https://mpra.ub.uni-muenchen. de/61147. [Date accessed: 07.12.2018].

Korotayev, A. 2018. The 21^st Century Singularity and its Big History Implications: A Re-analysis. Journal of Big History II (3): 71–117.

Korotayev, A., Malkov, A., and Khaltourina, D. 2006a. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: URSS.

Korotayev, A., Malkov, A., and Khaltourina, D. 2006b. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends. Moscow: URSS.

Kremer, M. 1993. Population Growth and Technological Change: One Million B.C. to 1990. The Quarterly Journal of Economics 108: 681–716.

Kurzweil, R. 2005. The Singularity is Near: When Humans Transcend Biology. New York: Viking Penguin.

Malthus, T. 1978 [1798]. Population: The First Essay. Ann Arbor, MI: University of Michigan Press.

McEvedy, C., and Jones, R. 1978. Atlas of World Population History. Harmondsworth, MX: Penguin.

NASA. 2014. Extending the Operational Life of the International Space Station until 2024: NASA Report IG-14-031. Washington, DC: NASA.

Panov, A. D. 2005. Scaling Law of the Biological Evolution and the Hypothesis of the Self-consistent Galaxy Origin of Life. Advances in Space Research 36 (2): 220–225.

Petigura, E. A., Howard, A. W., and Marcy, G. W. 2013. Prevalence of Earth-size Planets Orbiting Sun-like Stars. Proceedings of the National Academy of Sciences of the United States of America 110 (48): 19273–19278.

PricewaterhouseCoopers. 2017. The Long View: How Will the Global Economic Order Change by 2050? URL: https://www.pwc.com/gx/en/issues/economy/the-world-in-2050.html. [Date accessed: 19.12.2018].

Renfrew, C. 1984. Approaches to Social Archaeology. Edinburgh: University Press.

Ritchie, H., and Roser, M. 2018. Energy Production and Changing Energy Sources. URL: https://ourworldindata.org/energy-production-and-changing-energy-sources. [Date accessed: 18.12.2018].

Roser, M. 2018. Future Population Growth. URL: https://ourworldindata.org/future-population-growth. [Date accessed: 18.12.2018].

Roser, M., and Ritchie, H. 2018. Land Cover. URL: https://ourworldindata.org/land-cover. [Date accessed: 18.12.2018].

Sitwell, N. H. H. 1984. The World the Romans Knew. London: Hamish Hamilton.

Stent, G. S. 1978. Paradoxes of Progress. San Francisco: W. H. Freeman.

Turchin, P. et al. 2018. Quantitative Historical Analysis Uncovers a Single Dimension of Complexity that Structures Global Variation in Human Social Organization. Proceedings of the National Academy of Science USA 115 (2): E144–E151.

United Nations Development Programme. 2018. Human Development Reports. URL: http:// www.hdr.undp.org/en. [Date accessed: 24.12.2018].

United Nations, Department of Economic and Social Affairs, Population Division. 2017. World Population Prospects: The 2017 Revision. URL: http://esa.un.org/unpd/wpp. [Date accessed: 27.12.2018].

Warmington, E. H. 1995 [1928]. The Commerce between the Roman Empire and India. New Delhi: Munshiram Manoharlal.

Wikipedia. 2018. International Space Station. URL: https://en.wikipedia.org/wiki/International_Space_Station. [Date accessed: 20.12.2018].