Complication of Animal Genomes in the Course of the Evolution Slowed Down after the Cambrian Explosion

Introduction

The achievements of modern paleontology and paleogenetics allow to date more precisely the time of emergence of growing number of taxons. At the same time, with the development of DNA sequencing techniques, not only genome sizes but also its complete nucleotide sequences have been determined for an increasing number of species. The comparison of these data bases allows a more precise analysis of the dynamics of genetic systems development, that is the analysis of molecular processes that occurred on our planet in the course of the evolution of biological systems. Numerous studies are devoted to this interesting and attractive subject, in which the correlation between organism's genome size and the level of its evolutionary development has been studied and confirmed. Minimal genome size (MGS) is used as a quantitative criterion of this level that considerably determines genomic specific sequence and characterizes the level of organism's morphophysiological complexity.

In the present work we analyze the results published by Markov, Anisimov, and Korotayev (2010) in Paleontological Journal. The authors studied dynamics of MGS changes for representatives of nine taxon greatly different in their evolutionary position and used the models of three families: exponential, hyperbolic and double exponential of the form Ln(L) = Ae^–BτLn(C). According to the authors, biexponential form of hyperexponential growth is the most correct model to describe dynamics of MGS changes that allow authors to conclude on the basis of this model that MGS growth has autocatalytic character that seems disputable for us. The use of adjustable parameters in such models and ignoring the opposite process of suspension in the development and partial loss (disappearance) of the biota intrinsic for the evolution does not allow considering these models as the most appropriate to describe dynamics of organisms' MGS changes. Mathematical analysis of evolutionary processes in biology often operates with S-shaped curves whose character is stipulated by the presence and influence of counteracting processes. The most widely used S-shaped curves are represented by logistic curves and Gompertz curve.

We assert that the S-shaped curve with distinct inflexion point is the most relevant to reflect the pattern of experimental points arrangement given in the paper by Markov, Anisimov, and Korotayev (2010). In other words, MGS changes in the course of the whole evolutionary process (about 4 billion years long) should be considered as a multiphase process with exponential growth and a slowdown starting from a certain moment. We suggest the integrated mathematical model of development (IMMD) that allows to take into account the presence and influence of two inherent and opposite processes: the process of animal genome growth (when new species and higher taxons are formed) and the process of suspension in genome size development, stabilization of its size comparable with disappearance of some species and other taxons in evolutionary selection.

Material and Methods

Basic concepts and assumptions of the proposed integrated model

The proposed integrated model of development (IMMD) was previously successfully used to describe growth dynamics of unicellular organism populations in periodic and continuous processes and demonstrated its high adequacy (Klykov and Derbyshev 2009; Klykov et al. 2011; Klykov, Skladnev, and Kurakov 2012). The model incorporates three components.

А. Unstructured model previously developed by Derbyshev et al. (2001) allows calculating energy costs for growth and vital activity of population units, total maximum quantity of units accumulated in separate population and other parameters required for calculation in structured model.

B. Structured growth model just allows calculating the structure of growing population divided into two parts and including stable (resting) cells (stage В of cell cycle in prokaryotes, stages G₀ and G₁ in eukaryotes) and dividing (developing) cells at any stage of cell cycle except for the stages mentioned above. The main indicator of population structuring is determined as a ratio of the number of stable (resting) population units to the total number of population units. Such a model enables to determine the rate of stable cells accumulation and, accordingly, time of cessation of all cell divisions, that is the final time of development in specific conditions.

C. Model of metabolism allows calculating both dynamics of source nutritional elements consumption and dynamics of metabolites formation that are produced during life activity and, in turn, may be used as nutritional elements in certain conditions. Therefore, the model of metabolism for source nutritional elements and derived products is described by the same equation.

Unstructured and structured models of growth dynamics of biological objects – biomass (1) and also the model of their metabolite production or substrate consumption (2) have the following form:

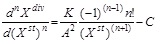(1)

and

where n is the integer number that determines derivative order of this function; X^div is the number of dividing cells; X^st is the number of resting (stable) cells; Р is the target metabolite product; S is a substratum; K is a product of total growth rate and the rate of stable (resting) cells accumulation; A is the ratio of energy for maintenance of life activity to energy consumed for biomass growth and/or the rate of stable (resting) cells accumulation. In addition, C = 1 if n = 1, and C = 0 if n ≥ 2.

The following symbols and assumptions are accepted for parameters required to use IMMD equations for MGS dynamics analysis:

1. Symbol Р denotes a product that is the animal MGS;

2. Symbol Х denotes an introduced parameter of Taxonomic Platform (TP), the object of taxa generation in the course of evolution when new species are formed;

3. Symbol Х^div denotess Taxonomic Platforms (TPs) that have undergone evolutionary process leading to MGS increase;

4. Symbol Х^st denotes TPs classified as: А-TPs, not subjected to evolutionary changes of MGS at present, and В-TPs, extinct by the present moment for natural reasons. The difference between A-TPs and B-TPs groups is in the fact that the first group consists of living populations and exists in nature in dynamic balance determined by equations for continuous processes (Klykov and Kurakov 2012).

Results

The results of animal genome evolution analysis conducted using IMMD are presented in Figs 1 and 2 in semilogarithmic and usual coordinates. Fig. 2 shows designed changes in TP number over 4 billion years.

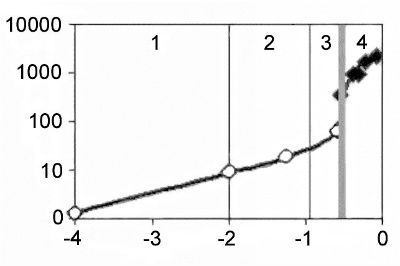
Fig. 1. Dynamics of animal MGS increase in the course of evolution. X-axis is time in billion years. Y-axis is MGS decimal logarithm according to data from Markov, Anisimov and Korotayev (2010). experimental data; –◊– data related to the pre-Cambrian period (Experiment + Model); data after the Cambrian explosion (Model); 1 – the 1^st phase of MGS growth; 2 – the 2^nd phase of MGS growth; 3 – the 3^rd phase of MGS growth; 4 – the 4^th phase of MGS growth; 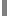– the Cambrian explosion

Fig. 2. TP accumulation in the course of evolution calculated according to IMMD. X-axis is time in billion years, Y-axis is TP units. – total number of TPs for both exponential phases; – TP number in dynamic balance, or extinct in exponential phase 2; and – number of evolving TPs in the 2^nd and 3^rd phase; – a total number of TP in slowing phase; and TP number in dynamic bal ance or extinct, in the exponential phase 2 and for the slow-ing phase; 1 – exponential phase 1 of TP number accumula-tion; 2 – exponential phase 2 of TP number accumulation; 3 – phase of TP number growth slowing after the Cambrian explosion; – the Cambrian explosion

The curve that reflects MGS increase during animal evolution has four distinct phases; the first three of them may be described by exponential models. The following stages and their characteristics are proposed.

1. 4–2 billion years ago: 1–2 TPs were formed, that is one completely and one partially changed; for TP μ_max = 0.0684 (billion years)^–1; MGS growth constant k^div = 5 nucleotide-base pairs (np)/1000 years/TP.

2. 2–0.942 billion years ago: μ_max is supposed to be increased 32 times in comparison with the first stage; for TP μ_max = 2.2072 (billion years)^–1, MGS growth constant k^div = 5 np/1000 years/TP.

3. 0.942–0.575 billion years ago: k^div was increased three times in comparison with the end of the second stage and approximately tenfold in comparison with the first stage; for TP μ_max = 2.2072 (billion years)^–1; MGS growth constant k^div = 15 np/1000 years/TP.

4. From 0.575 billion years ago up to the present: k^div increased 24 times in comparison with the end of the third stage and 73 times in comparison with the first stage; for TP μ_max = 2.2072 (billion years)^–1; A = 2.207 (billion years)^–1, for MGS growth k^div = 365 np/1000 years/TP.

The following equations are derived for MGS in the previous periods:

1^st phase: L₁ = 1.3 + 73.1 (e^{0.0684(τ + 4)} – 1), (3)

2^nd phase: L₂ = 9.03 + 2.47 (e^{2.0272(τ + 2)} – 1), (4)

3^d phase: L₃ = 23 + 7.4 (e^{2.0272(τ + 2)} – 9.03) – 136.63 [2.0272 (τ + 2) +

+ 9.03e^{–2.0272(τ + 2)} – 3.2], (5)

4^th phase: L₄ = 60 + 165.38 {47.29 Ln [23.65/(47.29 – X₄)] –

– (X₄ – 23.64)} – 1954.8 (X₄ – 23.64)/(47.29 –X₄), (6)

X₄ = 47.29 – 23.65e ^{–2.2072 (τ + 0.575)}, (7)

where Х₄ is TP number after the Cambrian explosion; L is the minimal genome size (nucleotide base pairs) × 10⁶; (τ + 4), (τ + 2), (τ + 0.575) – time (billion years).

Discussion

Substantiation of S-shape for the curve plotted by Markov, Anisimov, and Korotayev's points (2010)

Many processes occurring in Nature in closed systems with participation of living organisms with inconstant rate (varying from initially low rate to potentially maximum and descending to zero rate) are known to be graphically represented by S-curves and described by exponential equations and Equations (1), (2), with integral form shown in our previous publications (Klykov and Derbyshev 2009; Klykov et al. 2011; Klykov, Skladnev, and Kurakov 2012).

In our opinion, the arrangement of experimental points shown in Fig. 1 indicates the presence of inflexion point and decrease of MGS growth rate in the time segment after this point. In other words, the model of MGS growth dynamics should be represented by the curve with inflexion point or S-curve instead of exponential curve. The analysis of Markov, Anisimov and Korotayev's data according to IMMD has shown the presence of two exponential phases and a phase of slowing growth and further manifested high statistical reliability.

Substantiation of IMMD acceptability and analysis of MGS changes

Ascertained S-character of MGS dynamics is a reason to use IMMD where we suggest introducing the concept of Taxonomic Platform as an object of the most radical stage of the evolution of biological structures to designate the X parameter in Equations (1) and (2). The evolutionary changes of TP providethe basis for considerable increase in species diversity of organisms living in similar conditions in competitive situation. The increasing number of TP leads to a drastic increase in diversity of biota, development, stabilization or disappearance (extinction) of taxons. The concept of TP may be used as the basis to define and explain accelerating or decelerating mechanisms of evolutionary processes.

The task formulated above to find TP number from results of MGS measured as a product is an inverse task by its mathematical essence that has been solved in cell population kinetics calculations. The integral solutions of Equation (2) are transcendent. Hence, they cannot be solved algebraically unless the transcendence is eliminated. Therefore, the curve parameters have been found by iterative method. The time when the single unique TP existed on Earth (beginnings of life on Earth) is taken as zero point in calculations.

The activity and number of any TP depending on time are supposed to be described by the same Equations (1) and (2) as an evolutionary curve. As any other periodic process TP evolution may be finished either by a total extinction of corresponding populations (alternative B) or partial extinction followed by transition to a new taxonomic level (X^div) or to equilibrium condition (alternative A) described by continuous process equations (Klykov and Kurakov 2012) but with maintenance of all previous TP characters. Symbol k^div means specific constant of MGS increase in evolving TPs while k^st is corresponding specific constant of reverse (destructive) process. The subsequent analysis has confirmed the assumption of k^st = 0. When the system reaches equilibrium, the X parameter is equal to the equilibrium biomass of individual living taxa.

Thus, the first phase of MGS growth corresponds to the first exponential stage of new TP number growth. The second and third phases of MGS growth correspond to the second stage of TP number exponential growth. The fourth phase of MGS growth corresponds to decelerated phase of new TP number growth.

At the first exponential MGS growth phase the rate of new TPs formation is very low in comparison with the second exponential phase. At the second exponential TPs growth phase but at the third MGS growth stage, TPs corresponding to X^st may start to be formed. The rate of new TPs formation in the second exponential phase corresponds to their duplication every 340 million years. At the third MGS growth phase, corresponding to the age of the Cambrian explosion, the number of non-evolving TPs grew exponentially and the formation of total TPs number as well as MGS growth slowed down.

The statistical analysis has detected correlation factor R² = 0.9722 between experimental and calculated MGS values and R² = 0.9938 between logarithms that proves S-shaped character of MGS dynamics.

In our opinion, data obtained on TPs number calculated according to IMMD comply with available information on epochal evolutionary changes. They may include those TPs whose formation complies with the emergence of the following morphophysiological characters and properties expressed in the features of reproduction and development, extraction and production energy as well as coexistence and interrelations in the biota: DNA-RNA-protein mechanism; reproduction types; membrane systems; anaerobes and aerobes; eukaryotes; multicellular organisms; cell specialization, development of functional systems and organ differentiation (digestion, respiration, nervous system and sense organs, endocrine, hematopoietic, immune and other systems), mind, etc.

Conclusions

1. For the first time the growth rate of minimal genome size (MGS) is shown to slow down in the course of the evolution from prokaryotic forms to mammals after the Cambrian explosion. The S-shaped curve with distinct inflexion point is shown to be used to describe dynamics of MGS changes.

2. Stages of animal evolution are analyzed using original Integrated Mathematical Model of Development taking into account multidirectional processes in the course of MGS changes. The decreasing absolute rate of animal evolution after the Cambrian explosion is shown to be caused by the decrease in the rate of emergence of the evolving taxons number.

3. Different stages of MGS changes in the course of evolution and certain parameters of evolutionary processes revealed as a result of the model application are mathematically and biologically explained.

4. The concept of Taxonomic Platform is proposed and substantiated for analysis of the evolutionary process. This is a basic unit of radical step in suprapopulation biotic systems existing in certain conditions of interrelations and tending to development, stabilization and species (and other taxa) disappearance that underlines definition and explanation of accelerating and decelerating mechanisms of the evolution.

Acknowledgements

We are grateful to Dr. V. V. Derbyshev for the fruitful discussions about the Unstructured model.

Derbyshev V. V., Klykov S. P., Glukhov N. N., and Scherbakov G. Ya. 2001. Development of Cell Populations in Conditions of Energy Supply Limitation. Biotekhnologiya 2: 89–96.

Klykov S. P., and Derbyshev V. V. 2009. Dependence of Cell Population Age Structure, Substrate Utilization and Metabolite Synthesis on Energy Consumption. Biotekhnologiya 5: 80–89. In Russian (Клыков С. П., Дербышев В. В. Зависимость возрастной структуры популяции клеток, потребления субстрата и синтеза продуктов от энергетических затрат. Биотехнология 5: 80–89).

Klykov S. P., and Kurakov V. V. 2012. A New Kinetic Structured Model for Cell Cultivation in a Chemostat. BioProcess International 10(9): 38–43.

Klykov S. P., Kurakov V. V., Vilkov V. B., Demidyuk I. V., Gromova T. Yu., and Skladnev D. A. 2011. A Cell Population Structuring Model to Estimate Recombinant Strain Growth in a Closed System for Subsequent Search of the Mode to Increase Protein Accumulation during Protealysin Producer Cultivation. Biofabrication 3(4). doi: 10.1088/1758-5082/3/4/045006.

Klykov S. P., Skladnev D. A., and Kurakov V. V. 2012. A Model of Energy Limitation and Population Structuring to Estimate Phototrophic Growth of Industrially Significant Halobacterium Salinarum Strains. International Research Journal of Biochemistry and Bioinformatics 2(5): 109–121.

Markov A. V., Anisimov V. A., and Korotayev A. V. 2010. Relationship between Genome Size and Organismal Complexity in the Lineage Leading from Prokaryotes to Mammals. Paleontologichesky jurnal 4: 3–14. In Russian (Марков А. В., Анисимов В. А., Коротаев А. В. Взаимосвязь размера генома и сложности организма в эволюционном ряду от прокариот к млекопитающим. Палеонтологический журнал 4: 3–14).