Fission, Fusion and Quantisation in Global Political Evolution
Almanac: Globalistics and Globalization StudiesCurrent and Future Trends in the Big History Perspective
The article will show how an abstract theory of political evolution could be constructed using ideas from nonlinear dynamics. This is inspired by work on social macrodynamics that has proven the power of compact mathematical models for understanding global history. The features addressed are: quantisation of polity size; pathways of fission and fusion in response to Malthusian stress; the connections between population growth, resource pressure, conflict, and technological and institutional change.
Keywords: political evolution, macrodynamics, conflict, imperialism.
John Marc Widdowson, Independent researcher, Bourne, Lincolnshire more
This paper describes an approach to a mathematical model of long-term global political evolution. It is a sketch rather than a completed theory. It is inspired by the compact macromodels of global evolution developed by Korotayev, Malkov, and Khaltourina (2006a, 2006b). Such models capture the phenomenon in a few equations and variables, making them unambiguous and graspable by the human mind. The goal is deep, principled understanding, which would be supplemented by nuanced, contextual knowledge for real world situations.
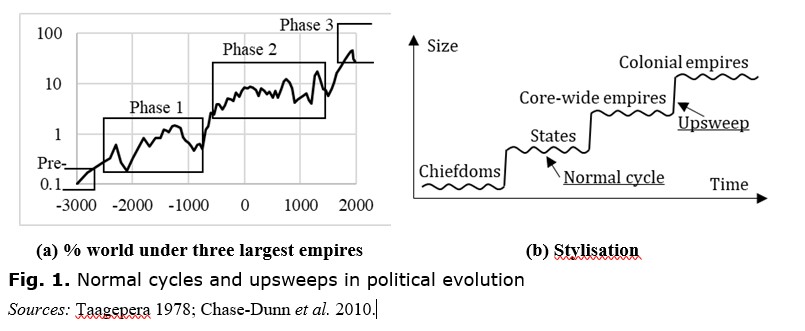
Several authors have found quantisation in evolution of political institutions. Taagepera (1978) noted a step-wise growth of empire sizes. Chase-Dunn et al. (2010) formalised this into a ‘normal cycle’, during which polities fluctuate around a typical size, and ‘upsweeps’, when the size abruptly increases (see Fig. 1). Korotayev and Grinin (Korotayev 2006; Grinin and Korotayev 2006) state that world urbanisation consists of a series of attractors (e.g., ‘complex agrarian society’) divided by transitional phases.
Henry Wright (2018) shows quantisation in the sizes of polities' largest settlements, which form discrete clusters rather than varying continuously (see Fig. 2). Fletcher (1995) also identifies quantisation of settlement sizes, which he attributes to a series of communications revolutions that made it possible to administer settlements of larger areal extent hence population, given limits on population density. Other illustrations of socio-political quantisation include Johnson on types of political official (Johnson 1982), Johnson and Earle on social evolution (Johnson and Earle 2006: 314), DeDeo on evolution of norm-observance (DeDeo 2017), Carneiro on levels of political integration (Carneiro 1987), and Korotayev and Grinin (Korotayev and Grinin 2006) on the typology of states.
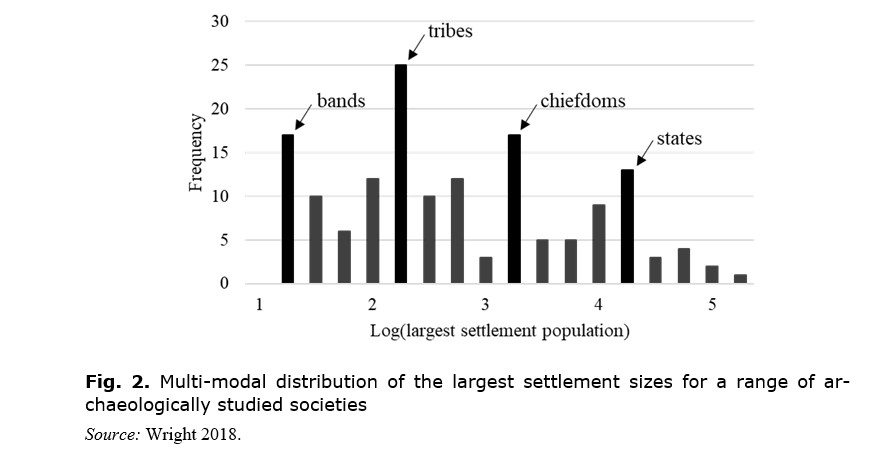
Thus, the quantum nature of political evolution manifests itself in population (Wright 2018), areal extent (Taagepera 1978), settlement size / urbanisation (Fletcher 1995; Korotayev 2006), and institutional complexity (Carneiro 1987; DeDeo 2017; Johnson and Earle 2006; Korotayev and Grinin 2006).
One way into understanding this is through Graber's work on political fission and fusion among a set of societies (Graber 1995). As population increases, the societies try to maintain constant density and size by splitting and dispersing, resulting in numerical proliferation and areal expansion. If this is not possible because there is no empty territory, then, according to Graber's ‘symmetry thesis’, societies fuse so that any increase in density is matched by an equal and opposite decrease in the number of societies. This is a mathematisation of Carneiro's circumscription theory of state formation (Carneiro 1970), but avoids the problem highlighted by Zinkina et al. (Zinkina, Korotayev, and Andreev 2016) that conquest is virtually absent from village-level societies since Graber makes no claim about how societies merge, only that they do.
We can understand fusion via Turchin's idea that ‘war’ encourages growth of ‘integrative factors’, which suppress war (Turchin 2016). Plundering of land and property, suggestive of pressure on resources, are prevalent in small societies (Zinkina, Korotayev, and Andreev 2016), and such conflict might eventually make people accept over-arching political institutions (integrative factors) that bind neighbouring societies together and settle their disputes. This shifts the focus from conquest by ambitious leaders to the mood and motivation of entire populations, that is in Tolstoy's imagery, from the Napoleons to the generalised ‘swarm life’ of humanity (Tolstoy 1957).
A striking feature of political quantisation is that the steps appear roughly equally spaced on logarithmic axes (see Figs 1a, 2;Korotayev 2006). It means the sizes of political units go up in a geometric progression.[1] This makes sense if N villages become fused into a chiefdom, N chiefdoms become fused into a simple state, and N simple states become fused into a complex state. Then the sizes of political units go up in the ratio 1:N: N2:N3. Such constancy in the number of fusing units suggests that conflict, and subordination to higher political control, operate in essentially the same way at each level, so one abstract model might cover all stages of political evolution.
From these findings and theories we can synthesise the picture of Fig. 3. We imagine a region, which might be the Amazon rainforest, a continent, or the whole world. It is occupied by polities, which we will call villages. As population grows, villages become oversized, resulting in more frequent disputes (Johnson 1982) until one faction leaves and sets up a new village. This is the normal cycle, when polities fluctuate around a typical size. Eventually, the whole region is filled. Now as population grows, disputes arise between villages, which are competing for a larger share of finite resources. The resulting conflict leads to fusion of villages into chiefdoms. This is the upsweep, that is emergence of a higher-level polity much larger than any previous ones. Such fusion of villages into chiefdoms goes on across the whole region, in another normal cycle, until all villages have been absorbed. At this point, there is no more space for chiefdoms, and there is another upsweep as chiefdoms fuse into simple states, and so on. Note that the deproliferation of villages is the same as the proliferation of chiefdoms, so in general fusion of polities at one level corresponds to fission of polities of the next higher level.[2]
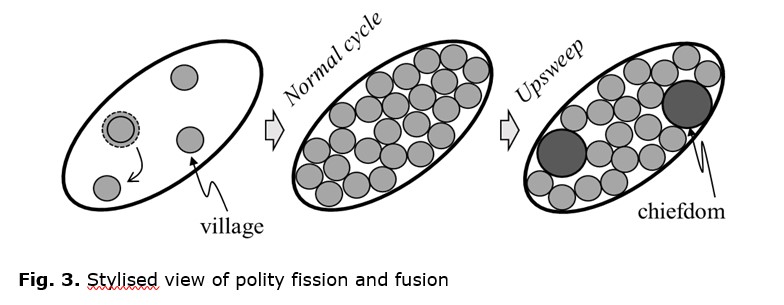
We might ask how fusion resolves conflict, since the underlying problem of overpopulation and resource competition would seem to remain. The answer is that political enlargement allows economic intensification, thus supporting a higher population on the same resource base. The fused population can specialise and invest on a larger scale. An autonomous village has only simple subsistence technologies, but chiefdoms, states and modern nations have metal-working, roads and consumer electronics that are not viable for a village alone. The carrying capacity of the fused polities is more than the sum of their individual carrying capacities, and a population that exceeded carrying capacity when divided into many polities can be less than the carrying capacity when they are combined. Specialisation also applies to political officials. A chiefdom can support a small standing army, which a village cannot. Hence fusion/enlargement reduces the causes of conflict (resource pressure) as well as providing more effective methods of managing conflict.
For the purpose of abstraction, we will say that a fused population supports a higher ‘technology’, which may include social technologies (institutions) as well as material ones. Abstractly, a technology is an activity network or organising principle for human behaviour, whether political, economic or cultural. (A smartphone is not really metal and glass but the app developers, microwave engineers and salespeople who make it a living technology.) Networks imply a loss of autonomy or a need to fit in with others, and are resisted until population pressure makes them necessary.
To represent the above argument mathematically, we suppose that population density, i.e. population Р divided by area А is linearly proportional to technology T (Widdowson 2020), so

This result concerns long-run envelopes of social processes. The higher carrying capacity depends on specialisation, which will not emerge instantly. Conflict will first be reduced by the new political institutions (e.g., chiefs or tribal councils) of the fused polity. Economic intensification will come later, and on even longer timescales there may arise group solidarity to replace coercion with co-operation in attaining social control.
We can now construct a generalised, abstract theory of political evolution. Our presentation will be neither entirely rigorous nor complete, and will leave open certain questions. It is, on the other hand, intuitive and easy to follow, and lays the ground for a more mathematically and conceptually challenging theory to come.
Quantisation emerges when a system's behavioural equations have periodic solutions. Here, we want to build a model where different levels of political complexity emerge, in a suitable phase space, as regularly spaced attracting fixed points representing periodic solutions to a set of equations (see Fig. 4), where the phase space dimensions are taken to be population density and population pressure, and remember that this describes a collection of societies not an individual society. The figure shows two possible trajectories within the phase space.
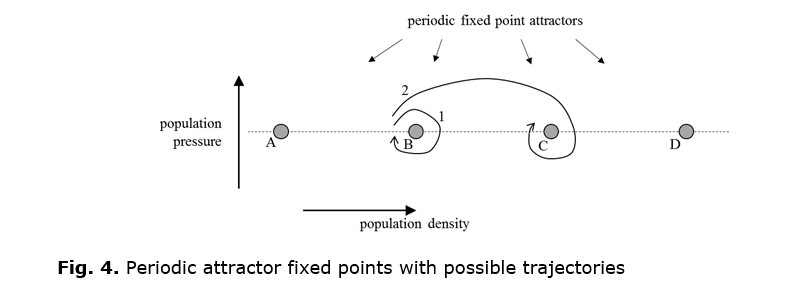
Trajectory 1 corresponds to the normal cycle. As population density increases, population pressure increases until societies start to split thus relieving population pressure. The resulting dispersal of societies into empty territory causes population density to stop increasing then to decrease. This further reduces population pressure so splitting ceases, which eventually reverses the decline of population density, and the whole process repeats.
Trajectory 2 represents an upsweep. In this case, population density and population pressure increase so rapidly that the collection of societies is carried away from fixed point B and becomes attracted to fixed point C. At C, the population density is higher than at B but the population pressure is the same, i.e. this represents the societies with the technologies necessary for higher density living.
A picture like that of Figure 4 emerges in the case of the rigid pendulum (see Figure 5).
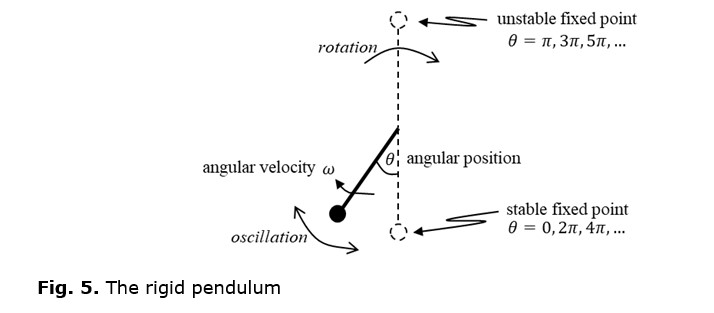
Stable positions occur when the pendulum is hanging vertically downwards, which we can see as a set of periodic fixed points at angles of 0, 2π, 4π, etc., i.e. when the pendulum has done 0, 1, 2, 3, etc. full revolutions. There are also unstable fixed points at angles of π, 3π, 5π, etc., when the pendulum is vertically upward, and these lie between the basins of attraction of the stable fixed points.
The equations that describe the pendulum are

References
Boserup, E. 1965. The Conditions of Agricultural Growth: The Economics of Agrarian Change under Population Pressure. London: George Allen and Unwin.
Carneiro, R. 1970. A Theory of the Origin of the State. Science 169: 733–738.
Carneiro, R. 1987. The Evolution of Complexity in Human Societies and Its Mathematical Expression. International Journal of Comparative Sociology 28 (3–4): 111–128.
Chagnon, N. 1997. Yanomamö. New York: Harcourt Brace Jovanovich. 5th ed.
Chase-Dunn, C., Niemeyer, R., Alvarez, A., Inoue, H., Lawrence, K., and Love, J. 2010. Cycles of Rise and Fall, Upsweeps and Collapses: Changes in the Scale of Settlements and Polities since the Bronze Age. In Grinin, L., Herrmann, P., Korotayev, A., and Tausch, A. (eds.), History & Mathematics: Processes and Models of Global Dynamics (pp. 64–91). Volgograd: ‘Uchitel’ Publishing House.
DeDeo, S. 2017. From Matter to Life: Information and Causality. In Walker, S., Davies, P., and Ellis, G. (eds.), Major Transitions in Political Order (pp. 393–428). Cambridge: Cambridge University Press.
Fletcher, R. 1995. The Limits of Settlement Growth. Cambridge: Cambridge University Press.
Graber, R. 1995. A Scientific Model of Social and Cultural Evolution. Kirksville, MO: Thomas Jefferson University Press.
Grinin, L., and Korotayev, A. 2006. Political Development of the World System: A Formal Quantitative Analysis In De Munck, V. C. Turchin, P., Grinin, L., Korotayev A. (eds.), History & Mathematics: Historical Dynamics and Development of Complex Societies (pp. 63–114). Moscow: URSS.
Johnson, A., and Earle, T. 2006. The Evolution of Human Societies. Stanford, CA: Stanford University Press.
Johnson, G. 1982. Organizational Structure and Scalar Stress. In Renfrew, C., Rowlands, M., and Segraves, B. (eds.), Theory and Explanation in Archaeology: The Southampton Conference (pp. 389–421). New York: Academic Press.
Kirch, P. 2002. The Evolution of the Polynesian Chiefdoms. Cambridge: Cambr. Univ. Press.
Korotayev, A. 2006. The World System Urbanization Dynamics: A Quantitative Analysis. In De Munck, V. C. Turchin, P., Grinin, L., Korotayev A. (eds.), History & Mathematics: Historical Dynamics and Development of Complex Societies (pp. 44–62). Moscow: URSS.
Korotayev, A., and Grinin, L. 2006. The Urbanization and Political Development of the World System: A Comparative Quantitative Analysis. In De Munck, V. C. Turchin, P., Grinin, L., Korotayev A. (eds.), History & Mathematics: Historical Dynamics and Development of Complex Societies (pp. 115–153). Moscow: URSS.
Korotayev, A., Malkov, A., and Khaltourina, D. 2006a. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: URSS.
Korotayev, A., Malkov, A., and Khaltourina, D. 2006b. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends. Moscow: URSS.
Taagepera, R. 1997. Expansion and Contraction Patterns of Large Polities: Context for Russia. International Studies Quarterly 41: 475–504.
Taagepera, R. 1978. Size and Duration of Empires: Systematics of Size. Social Science Research 7: 108–127.
Tolstoy, L. 1957. War and Peace. Tr. Edmonds R. Harmondsworth: Penguin.
Turchin, P. 2016. Ages of Discord. Chaplin, CT: Beresta Books.
Widdowson, M. 2020. Can Humanity Escape the Earth? In Grinin, L., and Korotayev, A. (eds.), History & Mathematics: Investigating Past and Future (pp. 184–227). Volgograd: Uchitel.
Wright, H. 2018. The Problem of States: The State of the Problem.In Sabloff, J. and Sabloff, P. (eds.), The Emergence of Premodern States: New Perspectives on the Development of Complex Societies (pp. 15–32). Kindle Edition. Santa Fe: Santa Fe Institute Press.
Zinkina, J., Korotayev, A., and Andreev, A. 2016. Circumscription Theory of the Origins of the State: A Cross-Cultural Re-Analysis. Cliodynamics 7 (2): 187–203.
[1] Figure 2 is about the largest settlement sizes not overall polity sizes. However, they are related. For an intuitive grasp consider that the ‘capital’ (largest settlement) provides functions for managing the entire polity, and so the size of the capital is likely to reflect the size of the polity. This is complicated by the existence, often in the New World, of administrative capitals that are distinct from the economic capital.
[2] Some fusion may be spontaneous. However, Polynesian chiefdoms are often set up by factions leaving an existing chiefdom (Kirch 2002), while many modern countries celebrate independence days, showing that they have arisen by fission as much as fusion.
