Potential Nested Accelerating Returns Logistic Growth in Big History
Almanac: History & Mathematics:Big History Aspects
Abstract
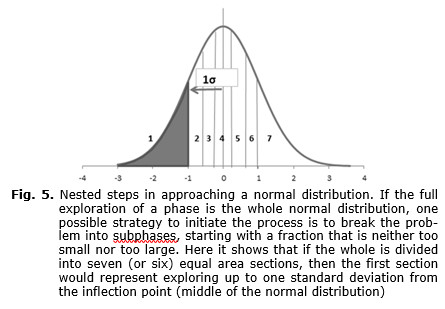
The discussions about the trends in rates of change, especially in technology, have led to a range of interpretative models including accelerating rates of change and logistic progress. These models are reviewed and a new model is constructed that can be used to interpret Big History. This interpretation includes the increasing rates of the evolutionary events and phases of life, humans, and civilization. These three phases, previously identified by others, have different information processing mechanisms (genes, brains, and writing). The accelerating returns aspect of the new model replicates the exponential part of the progress as the transitions in these three phases started roughly 5 billion, 5 million, and 5 thousand years ago. Each of these three phases might be composed of a further level of about six nested transitions with each transition proceeding faster by a factor of about three with corresponding changes in free energy flow and organization to handle the increased generation rate of entropy from the system. Nested logistic transitions have been observed before, for example in the ongoing exploration of fundamental physics, where the progress so far suggests that the complete transition will include about 7 nested transitions (sets of subfields). The reason for this number of nested transitions within a larger transition is not known, although it may be related to the initial step of understanding a fraction of the full problem. Too small of an initial fraction would lead to incomplete problem scope and definition. Too large of an initial step would lead to complications between the development of basic understanding and higher level derivations. An original step of one-seventh of the problem ends up within one standard deviation from the inflection point (mid-way through the transition).
Keywords: Big History, logistical growth, complex adaptive systems.
The forecasts of the near future vary widely in scope and outlook, predicting from near utopia to near dystopia. The issues of great concern during this period include: (1) the energy transition problem of moving from an unsustainable fossil fuel-based economy to something else; (2) the widespread nature of the problems currently being discussed in terms of global warming, global trade, global terrorism, and global knowledge transfer; and (3) the possible opportunities and risks of new technologies such as genetics, nanotechnology, and artificially intelligent computers and robots (Bainbridge and Roco 2005). To gain a wider perspective on this transition, this paper further explores the transitions involving energy, environment, leadership and new technologies (Tainter 1988; Diamond 1997; Ponting 2007; LePoire 2010a) in time scales from the current era, modern history, extended past, and potential future.
Recently, various interpretations of trends in technological progress have led to widely differing predictions. Specifically, Ray Kurzweil (2005) hypothesized an ever-increasing rate of technological change, based on his analysis of over a century of progress in computation technologies. Theodore Modis (2002) hypothesized a very different future, one having a decreasing rate of technological change, based on the analyses of events from the ‘Big Bang’ to the present. Kurzweil investigated the more recent technological acceleration of computing performance. The inclusion of early electronic technologies, such as relays and vacuum tubes, led Kurzweil to propose that the rate of technological change is increasing with time, that is, Moore's Law of the doubling of electronic device densities every 18 months will be surmounted by new technologies that double in performance in less time. An ever increasing rate of technological change could soon lead to a technological ‘singularity’. One attempt at
a definition of the technological singularity is a ‘future time when societal, scientific, and economic change is so fast we cannot even imagine what will happen from our present perspective, and when humanity will become posthumanity’ (Vinge 1993).
Another model of technology progression and diffusion that has been studied is based on the logistic equation. This progression assumes that the rate of progress is proportional to both the current level of complexity and the fraction of complexity yet to be discovered. Logistic analysis has been found not only in market adoption and substitution of new products, but also in technology development and ideas (Marchetti 1986, 1980) such as democracy and energy. Theodore Modis (2002) suggests that the history of the Universe might also be considered as a logistic development of complexity. He arranged important events in the history of the Universe from a variety of sources, assumed that each event was equally important, and then made the assumption that the complexity of an event is its importance divided by the transition time to the next event. The dependence of the cumulative fraction of complexity on milestone number (not the event's time) could be interpreted either as (1) the first half of
a logistic curve, or (2) a sequence of events that will culminate in a singularity. Modis favored the logistic development interpretation.
These two scenarios can be related to different simple models: Kurzweil's singularity scenario, with continual increasing exponential progress, might derive from a simple complex model, whereas Modis's long-term logistic growth with a tipping point determined by limitations in the learning rate and energy extraction rate, might be related to the more complex but realistic model. If this latter transition is accurate, the rate of technological progress might peak and eventually slow with impacts for economics and leadership (LePoire 2008, 2014).
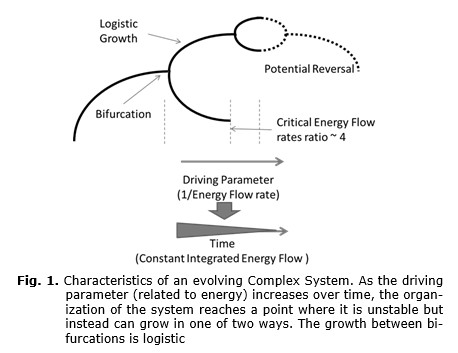
History may well form a large complex adaptive system (Jantsch 1980; Marchetti 1980; Perry 1995; Spier 1996, 2010). As systems progress, new options that arise for the systems may spontaneously bifurcate into two potential discrete states (see Fig. 1). While the simplest model of complex systems can be driven into chaos, more realistic models with limitations suggest a possible reversal of increasing complexity (Stone 1993). The emergent properties of an evolving complex system might display simple patterns despite the complicated underlying processes (Cohen and Stewart 1994). Another approach is to take a longer view of historical trends and phases. Carl Sagan (1977) presented the stages of information processing, progressing exponentially from the early Universe to the present day. These stages were the development of life, brains, and technology, starting with life origins about 5 billion years ago. A geometrical progression rate would suggest transitions from life evolution to brain evolution around 5 million years ago and further transition to civilization and technological development about 5,000 years ago. The characteristic properties of complex adaptive systems include: (1) a resource which drives the level of complexity, such as energy use (Chaisson 2004); (2) new options at critical stages along development paths (Jantsch 1980); and (3) competition and learning as the options are explored (Dyke 1987).
Complex adaptive systems are found in a variety of fields and display a range of common emergent phenomena, such as bifurcations or transitions (Kauffman 1995). These transitions occur when an input to the system, such as energy flow, increases beyond critical levels. Studies of physical systems far from thermal equilibrium suggest that the energy flow is important in the development of more complex organization. Chaos and adaptation have been investigated in many natural developing systems such as biological evolution, ecosystems, and social systems. In such dissipative systems order can spontaneously form only when the system is maintained far from equilibrium, as measured by the usable energy that flows through a system.
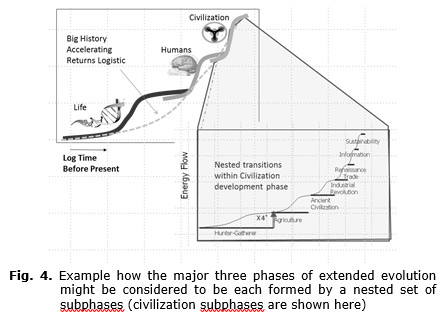
A time contraction factor of about 3 is similar to time and energy contraction factors found by Snooks (2005) and Bejan and Zane (2012). This time contraction factor was used in describing the changes in energy intensity (Fox 1988; Morowitz 2002; Niele 2005; Chaisson 2004; Smil 1994; Bernstein 2004), as summarized in Table 1. Note that just one time contraction factor was realized from the Big Bang to the beginning of life on Earth. The remaining three large phases of life, human, and civilization evolution are separated by bold lines with different shadings. Each of these major phases has five or six subphases. Note that six subphases with a contraction factor of the square root of 10 (about 3) give an overall contraction factor of 1,000 within each major phase.
Table 1. Possible way to organize changes in energy flows through extended evolution covering life, human, and civilization
development
|
Transition Start |
Description |
Energy Change |
|
15 Billion |
Gravitational |
Gravitational energy causes clumping and nuclear energy causes energy to be released and element formation |
|
5 Billion |
Planet/Life |
Life first gathers energy through chemicals or thermal gradients. Later the light from the Sun is captured and turned into chemical energy |
|
1.5 Billion |
Complex Cells |
Simple prokaryotes form symbiotic relationships to form a larger and more organized eukaryote cell |
|
500 Million |
Cambrian |
Oxygen levels reach a concentration so that multicellular organisms can be supported. The many body types and survival strategies lead to rapid evolution |
|
150 Million |
Mammals |
Animals move to land after plants. The larger temperature variations lead to a way to regulate temperature to ensure ability to be active throughout the day and seasons |
|
50 Million |
Primates |
A generalist strategy using various food so- |
|
15 Million |
Hominids |
Further generalist strategies and social organization again leads to greater energy use by the brain |
|
5 Million |
Humans |
Humans adapt to a changing climate by leaving the forest for the savannah along with the capability for walking to expand the range of natural resources |
|
1.5 Million |
Speech |
Further social organization leads to an expanded food sources including scavenging |
|
500,000 |
Fire |
Fire improves the energy availability from food |
|
150,000 |
Ecoadaptation |
Humans move out into other ecosystems expanding the range of energy resources |
|
50,000 |
Modern humans |
The benefits of specialization and social organization are realized during the ice age |
|
15,000 |
Agriculture |
Domestication of plants and animals leads to |
|
5,000 |
Civilization |
Organization at a city level allows risk reduction and order with increasing population |
|
1,500 |
Commercial Revolution |
Financial and mechanical technological techniques are applied and improved in a sustaining growth organization |
|
500 |
Scientific/ |
Exploration of lands and ideas leads to expan- |
|
150 |
Industrial |
Fossil fuel allows large amounts of resources to be used along with increasing specialization |
|
50 |
Information |
Control through systems and computers allows greater efficiency in the use of energy and handling of pollution |
There are similarities and differences between this interpretation and previous papers in this series. Specific issues include: 1) the nature of the current inflection point (Panov 2011); 2) the emphasis on non-equilibrium dynamics including bifurcation or energy, technology and also social organization (Nazaretyan 2011); and 3) the organization of evolutionary trends into two or three phases (Grinin, Korotayev, and Markov 2011).
Alexander Panov (2011) also organized evolutionary history with 19 evolutionary crisis transitions with decreasing duration (by about a factor of 3). This is called the scaling law of evolution. If the trend continues, evolution would come to a very rapid rate of evolution at some point in time, the Singularity, which was predicted to occur somewhere within the past two decades. However, as he notes, the rate of evolution cannot approach this infinite rate but instead would be constrained by resources and the ability for evolutionary processes to work by testing various environmental fitness of technologies and cultures. This is similar to the law of Accelerating Returns by Ray Kurzweil. However, just as normal logistic transitions first start with exponential growth and later slow due to limitations to form the S-curve transition, the hyperbolic growth of evolution might also begin to slow. The combined law of accelerating returns and the logistic developed here is one way to model this important inflection point in evolution, the ‘crisis of crises’ as stated by Panov. Such an inflection would indicate the conflict between conventional economic and resource growth and constraints of global resources, pollution, population, and conflicts.
Panov (2011) continues to discuss the possible ‘end’ of science. The complexity of the increasingly intertwined processes of science, development, and production might be reflected in the limits of scientific growth within the constraints of society. An outgrowth of this entanglement might be seen in the recent organization of technological hubs which combine research into the scientific basis, product development, and production of new technologies. For example, the U.S. Department of Energy has formed many exploratory technological innovation hubs to pursue new energy technologies such as energy storage (batteries) for both transportation and electrical grid buffering.
This nested logistical pattern, interpreted as alternating evolution of smooth exploration followed by intense reorganizing transitions is compatible with the view of Akop Nazaretyan (2011). He emphasized the non-equilibrium aspects of the evolution and the role of mental capacities to form new organizations that would lead through the crises to a new sustainable growth. It is not just the energy flow that increases complexity, but the ability to control the environmental impacts of that flow. Control was important in many transitions including the use of fire, the use of engineered water projects, and the current issues with potential climate change. He identified the 21st ‘bifurcation’ century as a test where a major inflection in the complexity, suggested by Big History, might raise many issues concerning conflict, energy, and the environment.
There is also the question of whether the evolutionary process occurred in three major phases discussed here – biological, human, and civilization, or two – biological and social phases as discussed by Grinin, Korotayev, and Markov (2011). The reason the phases were split into three in this paper is because of the three information storage and passing mechanisms identified (Sagan 1977), i.e. DNA, the human mind, and writing/artifacts. It is true that genetic changes were key in the development of humans but much of the learning was passed through social signals leading to the new tool of spoken language, while also beginning to control aspects of nature such as fire, dogs, and plants. Grinin et al. (2011) mention this aspect in the afterward of their paper by discussing intermediate subphases such as the biological-social type which would be similar to the human mind phase discussed here. Then the civilization, or pure social phase, is distinct because of the hierarchy of the social groups in combination with written records supporting the new organization.
Growth Pattern Characteristics
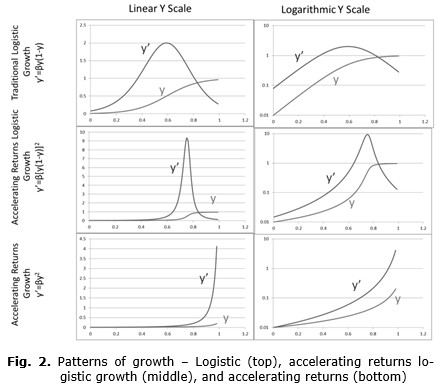
The first topic concerns the combination of accelerating returns model and the logistic model. The accelerating rate of return can be written y’ = ky2. This tends to grow faster than an exponential with a singularity at some point in time. The logistic equation can be written y’ = ky(1 – y), which has an inflection point but more linear progression of time scales. The super-exponential early growth can be combined with the logistic equation by combining the features of each y’ = k[y(1 – y)]2. This is shown in Fig. 2 in linear and log form. This is appropriate for a long-term development discovery system, whereas the simple logistic equation is more appropriate for diffusion of information. More insight can be gained by noting the exponential growth rate, y’/y, which is proportional to 1 – y for a traditional logistic growth, y for an accelerating returns growth, and y(1 – y)2 for the combination.
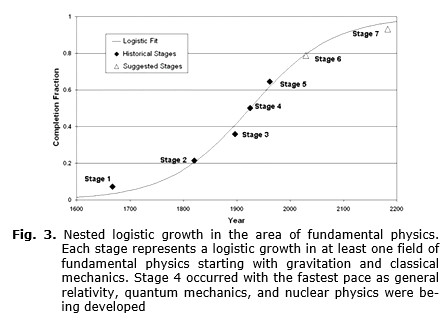
Why would a logistic transition be broken into 7 substeps? In the process of exploring a new field, one of the more difficult steps is the first in defining the subject, the scope, and process. While there were many discoveries in physics before Galileo, the sustained nature of scientific progress afterwards points to this difficulty. Some difficult concepts to frame were inertia – bodies tend to keep on moving, the relationship between force and acceleration (versus the force in the static mechanics). This led Galileo to the experiment with simple toy-like apparatus' like rolling balls down inclined planes and measuring objects at the end of strings. If the first step was in the wrong direction, too small or too large, the progress could be halted. Some of the Greek philosophers tried to solve everything in one hypothesis but were not able to defend it with measurements. If Galileo had observed the moons of Jupiter and then asserted the laws of the heavens had inertia but that did not apply on Earth, the rolling balls down incline planes would not have generalized the concept, i.e. it would have been too small. Instead the first phase of fundamental physics was the idea of laws of motion that applied on Earth and in the sky was set out by Galileo and took about 150 years through the great mathematics of the 18th century to develop the tools such as calculus, variational calculus, wave theory, and generalized laws of motion such as the Lagrangian. These tools that were developed in the first phase would become instrumental in further developments, for example, the Lagrangian formulation was instrumental in quantum mechanics whereas Newton's laws were found only applicable in classical mechanics.
One way to project what a logistic world would look like after the inflection point would be to mirror past rates of change. For example, if 2000 was the inflection point, meaning that technological change continues for a while at the same rapid progress but does not accelerate, then the 20th century might be a good indication of some of the changes we might see in the 21st. In the 20th century there was such growth in population and resource use to move the world beyond sustainability. The major energy supply was from non-renewable fossil fuels. The expansion was driven by relatively inexpensive energy, new insights from physics leading to electrical, aerodynamic and material technology. These innovations led to creative destruction in capital formation and development as exemplified by the semiconductor industry which followed Moore's Law. The technology also caused problems such as arms races, environmental impacts, and expensive medical options. The 21st century might adjust by slowing to a more sustainable society with more efficient energy use, a stable or declining population, reduction in the gap between incomes, and exploration of ways to mitigate global environmental impacts while maintaining robust fair trade.
While there are possible indications that a large transition such as a general technological slowdown is underway (LePoire 2014) there are reasons why we might be experiencing a transition inflection point in general evolution from a bootstrap natural evolution type system to a technologically design driven evolution which might show initial speed in development and then slow as leadership is assumed.
The problems with a bootstrap natural selection is that it has a difficult beginning and is stuck in historically determined structures, for example, the long period (billions of years) between the development of simple life and earth and multicellular life during the Cambrian explosion. The energy mechanisms, information storage and expression of biological systems were determined and mostly stable throughout further development. The systems also have difficulty scaling due to individual perspectives and limited information resources for collective action but instead are good at individual exploration, competition, and growth. The techniques for dealing with uncertainty are intuitive and based on evolutionary trajectories, for example, a simple intuitive fight or flight mechanism.
The assumption in the technological singularity is that technology will be able to quickly resolve human and biological constraints and continue an exponential growth path. However, this is unlikely as many constraints are tied to human systems and are also filled with uncertainty which might be better handled but will not be eliminated.
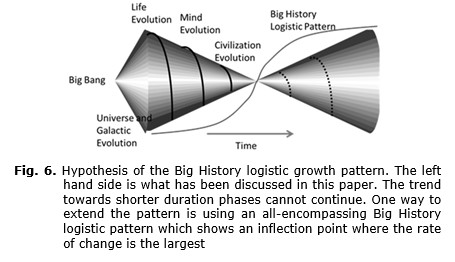
On a much longer time-scale the reflection of the rate of change would look something similar to Fig. 6. This paper focused on the left cone which includes the three phases (shown on a log time scale) of life evolution, human evolution, and civilization. If this follows the large logistic trends identified, the pattern in the future would look something like the cone on the right, again three phases with the characteristic slowing-down. However, it is not clear how and whether the logistic development pattern will continue.
Conclusion
The three major phases after cosmological development (i.e., life, human, and civilization) had durations of about 1,000th that of the previous. Each might have six subtransitions with durations being reduced by a factor of 3. Energy and organization might qualitatively change between the transitions to handle the additional entropy flow through the systems. These characteristics seem to be consistent with the interpretation of a complex adaptive system with evolution through a sequence of bifurcations and logistic learning. A logistic accelerating rate of return logistic pattern, formed by combining the accelerating rate of return growth and the traditional logistic growth pattern shows similar exponentially shorter transitions. The pattern eventually reverses as has been observed in ecological systems. The decomposition of each phase into six transitions is motivated by the reorganization to maintain increasing energy flows. This nested logistic transition has been observed in the history of the discoveries in fundamental physics. While it is not known why a nested logistic transition would decompose into this number of subtransitions, it was observed that with seven subtransitions, the first step explores up to one standard deviation of the inflection point. Future inflection, symmetrical from boot-strapped to engineered system may gain more control over energy and physical systems.
References
Bainbridge W. S., and Roco M. 2005. Managing Nano-Bio-Info-Cogno Innovations: Converging Technologies in Society. Springer.
Bejan A., and Zane J. P. 2012. Design in Nature: How the Constructal Law Governs Evolution in Biology, Physics, Technology, and Social Organization. New York: Doubleday.
Bernstein W. J. 2004. The Birth of Plenty: How the Prosperity of the Modern World Was Created. New York: McGraw-Hill.
Chaisson E. J. 2004. Complexity: An Energetics Agenda; Energy as the Motor of Evolution. Complexity 9(3): 14–21.
Cohen J., and Stewart I. 1994. The Collapse of Chaos: Discovering Simplicity in a Complex World. New York: Viking.
Diamond J. M. 1997. Guns, Germs, and Steel: The Fates of Human Societies. New York: W.W. Norton & Co.
Dyke C. 1987. The Evolutionary Dynamics of Complex Systems: A Study in Biosocial Complexity. New York: Oxford University Press.
Fox R. F. 1988. Energy and the Evolution of Life. New York: W. H. Freeman.
Grinin L. E., Korotayev A. V., and Markov A. V. 2011. Biological and Social Phases of Big History: Similarities and Differences of Evolutionary Principles and Mechanisms. Evolution: A Big History Perspective / Ed. by L. E. Grinin, A. V. Korotayev, and B. H. Rodrigue, pp. 158–198. Volgograd: Uchitel.
Jantsch E. 1980. The Self-Organizing Universe: Scientific and Human Implications of the Emerging Paradigm of Evolution. New York: Pergamon Press.
Kauffman S. A. 1995. At Home in the Universe: The Search for Laws of Self-organiza-
tion and Complexity. New York: Oxford University Press.
Kurzweil R. 2005. The Singularity is Near: When Humans Transcend Biology. New York: Viking.
LePoire D. J. 2005. Application of Logistic Analysis to the History of Physics. Technological Forecasting and Social Change 72(4): 471–479.
LePoire D. J. 2008. Exploration of Connections between Energy Use and Leadership Transitions. Systemic Transitions: Past, Present, and Future / Ed. by W. Thompson, pp. 205–222. New York: Palgrave Macmillan.
LePoire D. J. 2010a. Long-Term Population, Productivity, and Energy Use Trends in the Sequence of Leading Capitalist Nations. Technological Forecasting and Social Change 77(8): 1303–1310.
LePoire D. J. 2010b. Exploration of Energy and Environment Roles in Driving Large-Scale Historical System Transitions. Integrating Complexity: Environment and History. London – Ontario: University of Western Ontario.
LePoire D. J. 2014. Potential Economic and Energy Indicators of Inflection in Complexity. Evolution: Development within Big History, Evolutionary and World-System Paradigms / Ed. by L. E. Grinin, and A. V. Korotayev, pp. 108–118. Volgo-grad: Uchitel.
Marchetti C. 1980. Society as a Learning System: Discovery, Invention, and Innovation Cycles Revisited. Technological Forecasting and Social Change 18: 267–282.
Marchetti C. 1986. Fifty-Year Pulsation in Human Affairs: Analysis of Some Physical Indicators. Futures 18(3): 376–388.
Modis T. 2002. Forecasting the Growth of Complexity and Change. Technological Forecasting and Social Change 69: 377–404.
Morowitz H. J. 2002. The Emergence of Everything: How the World Became Complex. New York: Oxford University Press.
Nazaretyan A. P. 2011. Mega-Evolution and Big History. Evolution: A Big History Perspective / Ed. by L. E. Grinin, A. V. Korotayev, and B. H. Rodrigue, pp. 82–100. Volgograd: Uchitel.
Niele F. 2005. Energy: Engine of Evolution. Amsterdam – Boston: Elsevier.
Panov A. D. 2011. Post-Singular Evolutions and Post-Singular Civilizations. Evolution: A Big History Perspective / Ed. by L. E. Grinin, A. V. Korotayev, and B. H. Rodrigue, pp. 212–231. Volgograd: Uchitel.
Perry D. A. 1995. Self-Organizing Systems Across Scales. Trees-Structure and Function 10(6): 241–244.
Ponting C. 2007. A New Green History of the World: The Environment and the Collapse of Great Civilizations. New York: Penguin Books.
Sagan C. 1977. The Dragons of Eden: Speculations on the Evolution of Human Intelligence. New York: Random House.
Smil V. 1994. Energy in World History. Boulder: Westview Press.
Snooks G. D. 2005. Big History or Big Theory? Uncovering the Laws of Life. Social Evolution and History 4(1): 160–188.
Spier F. 1996. The Structure of Big History from the Big Bang until Today. Amsterdam: Amsterdam University Press.
Spier F. 2010. Big History and the Future of Humanity. Chichester – Malden, MA: Wiley-Blackwell.
Stone L. 1993. Period-Doubling Reversals and Chaos in Simple Ecological Models. Nature Cell Biology 365: 617–620.
Tainter J. A. 1988. The Collapse of Complex Societies. Cambridge – New York: Cambridge University Press.
Vinge V. 1993. The Coming Technological Singularity: How to Survive in the Post-Human Era. Proc. Vision 21: Interdisciplinary Science and Engineering in the Era of Cyberspace: 11–22. NASA: Lewis Research Center.
