The Chandra Multiverse
Almanac: History & Mathematics:Big History Aspects
Abstract
Equations of Planck and Chandrasekhar lead to our universe being a member of a quantized system of universes, the ‘Chandra Multiverse’. It is a trial-and-error evolutionary system; all universes have the same critical mass and finely tuned physics that our universe has. The origin and demise of our universe are described. In our astronomical environment everything ages and decays; even the proton may have a limited half-life. The decay products of all the universes expand into the inter-universal medium (IUM), clouds form in the IUM, from which new universes are started. When the density at the center of our proto-universe cloud reached proton density, photons, protons and neutrons were re-energized. A Photon Burst marks the beginning of our universe, 10–6 s, i.e. 1037 Planck times, later than a Big Bang; the evolution of forces, sub-atomic particles, and finely tuned physics, occurs in the Chandra Multiverse. This paper is based on 30 observations, 8 previous papers, and 2 books; the multiverse makes the identification of dark energy and dark matter possible.
Keywords: Universe, Chandra Multiverse, Planck Time.
To leave the earth's surface was the desire of Leonardo da Vinci – in 1783,
the first balloonists left the earth! There were four flights that year, from the squares of Paris, in full sight of thousands of people who had come out to see the miracle: ‘If we can do that, what can we not do?’ The French Revolution began soon after that. Of the next step, to the moon, President John F. Kennedy spoke to the US Congress in 1961. It sounds like poetry when you read it aloud:
I believe that this nation
should commit itself
to achieving the goal
before this decade is out,
of landing a man on the Moon
and returning him safely to Earth.
It was done, and had the same effect on the world population as on the people of Paris before. The trials and failures, and ultimately the flights and walks on the moon were shown on international television, in newspapers and magazines, watched and discussed by millions on Earth: ‘If we can do that, we can do anything!’ The astonishing feat of people leaving Earth may have spurred the surge of activity and questioning that took place during the ‘Great Sixties’ all over the world.
These two examples of broadening the horizons stimulate the Chandra Multiverse[1] to solve old problems and open new disciplines (‘Chandra’ was used by his colleagues and for the Chandra X-Ray Observatory spacecraft). There was an inkling of high expectations in 1954 when I was a student in the class of Subrahmanyan Chandrasekhar (1910–1995) at the Yerkes Observatory of the University of Chicago. There were many equations and derivations, but his cosmic-mass equation was exceptional because of its unified operation of quantum, relativity, gravity, and atomic physics. He hinted the possibility of deeper relations between atomic theory and cosmogony.

It took me years of preparation, but when I finally dared to use that equation, it pointed to our universe not being alone but being a member of the Chandra Multiverse with many others, each with the same mass and physics. I published that in 2007, and thought I was done, because others would surely jump to such a basic change in our worldview. No one stirred, so that I proceeded with various papers[2] and two books (Gehrels 2011, 2012). This is a beginning, a sketch to show possibilities, while expansion by specialists is needed for all parts.
Better understanding of the vast dimensions of the Chandra Multiverse follows from changing scales, using various measuring sticks. We use centimeters or inches for small distances on the desk, but it would be silly to use the large number of centimeters for going home, so that we switch to kilometers or miles. Beyond the Earth and Moon, the astronomical unit (AU) is used, which is the average distance of the Earth from the center of the Sun. To the outer edges of the solar system that becomes a large number again – 100,000 AU. So, beyond that to the stars and galaxies we use the light-year, which is the distance light travels in a year, ~1013 km.
In order to help you visualize the multiverse, consider the next larger grouping after planets and stars, which is a galaxy, the ensemble of at least a thousand million stars, and then the next step, another thousand million galaxies to populate our universe. Having come to the end of our universe, as far as we can observe it, we ask: ‘Why would our universe be the only one?’ Some theoreticians have already made models regarding the existence of other universes, but this article is about a specific set of universes. It is based on the mass equation of Chandrasekhar (1951) and is therefore called the ‘Chandra Multiverse’; it has nothing to do with any previous usage of the word ‘multiverse’.
This paper is all assembled for historians who call themselves ‘Big Historians’ for wanting to go back all the way in time. The evolution in the Chandra Multiverse is now the earliest we can go back to – there never was a Big Bang – and the early evolution is now properly taken care of in the multiverse.
Big Bang, Planck Time, Inflation and Strings
The words ‘Big Bang’ are commonly used for the beginning of our universe. As it is conceived, a supercharged explosion created the basic matter and energy that evolved over the course of 13.7 thousand million years into what we perceive to be our universe today. These Big Bang words are also used in a presently accepted theory called the ‘Standard Model’. In this model, our universe is generally believed to be the only universe... this is it for the Cosmos.
There are problems with this concept. The usual thinking is to reverse the expansion of our universe as a contraction back in time. A problem arises when one continues the contraction, without stopping, until all of the mass of our universe is in nearly zero space and compressed into nearly infinite density. That infinite condition is called a ‘singularity’, which has caused theoreticians to write a large amount of literature in papers, books, and encyclopedias. The Big Bang is believed to be confirmed by three observations, but these were made at ages of minutes and much later, applying nicely to the Chandra-Multi-verse model.
The Big-Bang starting time for the Standard Model is t = 10–43 sec and all of our basics would have had to be produced during the very beginning of our universe. The earliest stages after the Big Bang would have had to be able to evolve quantum mechanics, relativity, gravity, and atomic physics, as well as fundamental forces.
The Standard Model is that the volume of the universe must have stayed small for a while because of the condition that interaction must have flourished; in other words, everything could interact with everything else in such confinement. This requirement emerged when the background radiation between the stars was observed by the COBE spacecraft to have the same temperature of 1.728 K in all directions – the universe is uniform on its largest scales. However, this leads to that impossible early condition, because in order to interact, the components must be close enough. All of the quantum fluctuation components, with a total mass equivalent to 1021 solar masses, would have had to be confined in a volume so small that all their components could interact with all others at the velocity of radiation. Their density would have had to be as high as the Planck density of 1096 kg/m3, which does not seem realistic.
At this point of reasoning, inflation theory seemed to solve the problems in the 1970s, with a complex homogenizing and processing between 10–43 sec and 10–32 sec, removing a variety of uncertainties in the understanding of the early stages for our universe. (That interval is hard to imagine, and looks brief, while it is actually long for the fast subatomic actions. The usage of the second as a unit of time is better replaced here for sub-atomic action by the Planck time, which is about 10–43 sec. That interval is then [10–32 – 10–43] / 10–43 ~ 1011 PT.) Anyway, the inflation theory has in that interval a fast increase in the size of the universe, an inflationary expansion, with thorough interaction of components, explaining the uniformity of our universe found by COBE. This fast expansion was confirmed in later observations by the WMAP spacecraft (Spergel et al. 2007).
Such confirmation has not yet happened for string theories, which have no observations supporting them; they may be too small and energetic. String theories consider sub-atomic particles as one-dimensional curves called ‘strings’. The strings all differ in order for their vibrations to represent the variety of properties of sub-atomic particles. They facilitate storage of information by having those particles replacing the infinitely small point-particles of quantum theory. The theories are mathematically expressed and are powerful because they can describe atomic forces and fields; the strings are imagined to be embedded in space-time. They come in various sizes and shapes for storing the various properties; they may be curled and imperceptibly small. The variety of particle properties is a reflection of the various ways in which a string can vibrate: electrons vibrate in one way, quarks in another, etc. Several dimensions are added, at least seven, to the four we are used to (which are up-and-down, close-and-far, left-and-right, and time). The seven higher dimensions are not defined; no one seems to be able to describe them other than by making a comparison with the four (Randall 2005, 2007; Smolin 2007).
There are many string theories, Smolin gives their number as 10500, and the name ‘M-theory’, M for Many, is therefore used for the ensemble. There is some collaboration of inflation and string theorists, while there seems to be a general acceptance that some combination of inflation and strings is what happened at the beginning of our universe. Large physics departments have at least one inflationist and a string-theorist in their faculty; hundreds of physicists work on these theories in international collaboration.
Physicist Brian Greene has provided an overview of string theories and their history, and he revels in an analogy with vibrational patterns of music, how the strings orchestrate the evolution of the world into a cosmic symphony (Greene 1999).
Physicists Paul Steinhardt and Neil Turok criticize inflation theories, while presenting a string theory that has our universe pulsating, expanding ↔ contracting; they do not believe inflation theories (Steinhardt and Turok 2007). Physicists Peter Woit and Lee Smolin do not believe in string theory (Woit 2006; Smolin 2007). Steinhardt specifies why he finds inflation theory deeply flawed (Steinhardt 2011). Such is the state of affairs for understanding the early stages of our universe before t ~ 10–6 sec, the beginning time of our universe in the Chandra-Multiverse model, which has the earlier sub-atomic evolution in its multiverse.
Parallel Universes and Anthropic Principles
In the large literature about other multiverses, some of it seems to be anthropic (from the Greek anthropos, human being), i.e. based on human interpretations of physics. The anthropic principle has the idea that nature is the way it is because we are here to observe it – it was created for people. For example, physicist Hugh Everett (1971) adopted the wave interpretation of quantum mechanics held by Schrödinger and others (Bitbol 1995), but he also felt that this picture makes sense only when observation processes are treated within the theory. He favored an interpretation of quantum theory by which reality is brought through observation or measurement. Some of the literature about the multiverse is therefore based on an interpretation of quantum mechanics in which observations bring reality. I cannot help thinking of that when crossing a major street on the bike, ‘Perhaps if I just do not observe an oncoming car, it would not exist’, but I have not tried it yet. Books and articles describe various multiverses; some have ‘parallel’ universes with identical copies of us reading this paper at this time (Everett 1971; Vilenkin 2006). In contrast, the Chandra-Multiverse model is free of anthropics.
Expansion of 100 % Space
The word ‘space’ is a most frequently used word, while we actually
do not know what it is, in a physical sense. The best feel for space can be
obtained by a thought experiment: Imagine that the outer perimeter of the
hydrogen atom with its electron shell is as large as the longest outer
dimension of an Olympic stadium. How large is then the proton nucleus of the
atom on center field? As the size of the stadium is roughly three times the
length of a soccer or football field (100 meters or 300 feet), take the long
dimension to be about 1,000 feet, which is 103 x 12 (in/foot) x 2.54 (cm/in) =
3 x 104 cm.
Divide that by the known factor between the radii of
the hydrogen atom and the proton, 105, and it follows that the
nucleus would be 0.3 cm,
the size of a pea. All around inside that stadium is modeled as space.
Furthermore, the proton is a structure of space as well. So, the answer to the
question of how much of this atom is ‘space’ is 100 %. The most astonishing
conclusion is that this applies to all
atoms, to our entire visible world consisting of 100 %
space.
You might protest that the objects around us are solid and we experience our mass and weight – how can that be if we are 100 % space? The answer is that space has an abundance of particles with their properties. The word ‘particle’ is confusing because it reminds us of a solid grain. When physicists use the word, however, they do not mean anything like the Greeks did (an inert grain of dull matter), but rather that a particle is a point in space that produces a phenomenon, like mass. By what it does, a particle is something that provides action and an effect, like electricity. Both sentences together may help us understand the particles as forms of space and waves by which they produce and interact with gravity, electromagnetism, etc. It is because of the properties of particles and photons that we experience weight and all other characteristics of nature.
In this paper there is also much discussion about the expansion of space. It is simple to understand by the galaxies having been pushed apart and still moving because there is little to stop them. It may be helpful to imagine a cake in the oven, which expands as the temperature increases. Imagine yourself to be one of the raisins and you see the others drifting away... that is the expansion. A raisin twice as far away will seem to expand at twice the speed.
The First Minute of Our Universe
As of the notable event in the Standard Model that we mentioned at 1011 PT after the Big Bang, high-energy particle physicists begin to understand the physics involved at this time, just barely, and make proposals for the forces and sub-atomic particles that subsequently evolved. A feature of the theories indicates that particles formed symmetrically with their anti-particles of opposite properties. The two would then have largely annihilated each other. However, it was apparently not a total annihilation; one of the two types would have prevailed a little, and that survivor is what we now call a ‘particle’. It will be interesting to see if this feature of the theory survives in the evolution of the Chandra-Multiverse.
The next milestone came at 1031 PT with the emergence of four nuclear forces: the weak, gravitational, electromagnetic and nuclear forces. The forces and their laws began to be recognized in physicists' modeling of the temperature and pressure of that time.
At 1037 PT, protons and neutrons were made; a large amount of radiation was produced. We will see later that this is the beginning time for the Chandra-Multi-verse model, t = 0 for that model, and from here onwards the Chandra-Multiverse model adopts and follows the Standard Model. The evolution during the earlier 1037 PT is however in the multiverse; that is not an ad hoc assumption, but based on the realization that the early evolution, the natural selections, could not have happened in a single universe with fast changes in their environment, while in the multiverse there are many samples and long times like Darwin had for his finches and people. An example of natural selection is in Fig. 2, that is of course for millions of years later and still happening today.
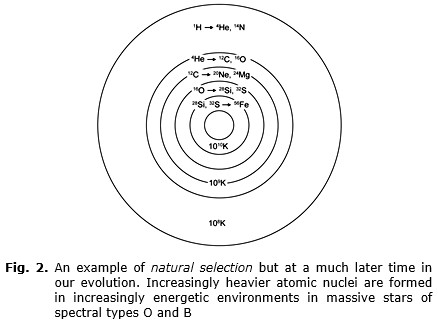
About the following millennia we know little, other than that the universe consisted of photons being scattered around by protons, electrons, etc. – a noisy and energetic mass in expansion, too dense for light to escape (except, perhaps, an early Photon Burst, we shall see). Not much was happening excluding this multiple scattering of light, somewhat similar to what happens inside the Sun, where it takes a million years for a newly made photon at its center to be bounced to the outer levels and then onwards to Earth. All we can do with the present models is to consider the plasma 380,000 years later.
The Universe at Age 380,000
Finally, at t = 380,000 years, came the last remarkable event of the Standard Model for the Big Bang. A great transition took place when the temperature and pressure reached a level at which the scattering diminished, resulting in less density such that the photons were knocked about far less violently and frequently. As a result, the nuclei (of protons and neutrons) and the electrons no longer had enough collision energy to stay free, so they coalesced into hydrogen and helium atoms, which are widely spacious to let the photons pass through them, as was mentioned two sections before.
By the time the expanding universe had reached the temperature of about 3,000 Kelvin, it resulted in the separation of matter and radiation. The radiation from that stage is still observed today. It is all around us, observed far away between the stars to where it has expanded since t ~ 10–6 sec. By now, the cloud has cooled to almost absolute zero. It is called the 3-degree-Kelvin radiation, 3 K being its approximate temperature. The COBE and WMAP spacecraft confirmed this. WMAP also derived that the detailed formation of galaxies and their stars began some 200 million years after the beginning of the universe. The galaxy formation peaked about 5,000 million years after the beginning, which is at 5×109 years of age for the universe, compared with the present age of 13.7×109 years (Spergel et al. 2007). The epoch of 5×109 years will return in the history of our universe, when the acceleration of the expansion was discovered.
Galaxies
Here is another thought experiment. Imagine that you are a galaxy in space... rather lonesome because space is so large and dark... but still, your gravity will make you move towards whichever galaxy wins over the gravitational tugging by all the others, because it may be closer or more massive. That is how the Andromeda Galaxy is moving towards our Milky Way Galaxy. Such gravitational interaction causes the galaxies' motion, groupings, clusters, and collisions.
Although nearly all galaxies expand away from us, they themselves do not expand (nor do we): galaxies have their own gravitational regime. The expansion takes place between the galaxies, and is therefore properly referred to as expansion of intergalactic space.
With the naked eye we can see at a certain place in the sky a ‘Milky Way’ band encircling the sky with the multitude of stars in the galaxy (Fig. 4). We see that because our solar system lies in the flat galaxy that from the outside would be seen in the shape of a discus (Fig. 3). The solar system is also about halfway from the center to the outer rim, and so we see more stars in the direction towards the galactic center than in the opposite direction. Now, if we look in the third direction, away from the plane of the Milky Way, up and down in the paper of Fig. 3, we see fewer stars that belong to our own galaxy and more of the dark sky because we look deep into space where there are few disturbing stars in our own galaxy or its halo. Now we can see other galaxies in the distance.
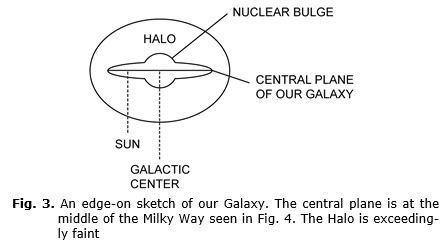
How large is our galaxy? At the speed
of light, it takes about 26,000 years to travel to its center, from the sun to
the right in Fig. 3. We are roughly
24,000 lightyears
away from the outermost visible stars in the other direction, to the left; this
is approximate, because there is no sharp
edge to the galaxy. We therefore are located a little more than halfway from
the center to the edge of our galaxy; the diameter of the galaxy is
about 100,000 (105) lightyears.
Galaxies occur in groupings. Outside of our Milky Way, we first encounter others of our Local Group, which has about 30 members and is about three million lightyears in size. The local groups are members of clusters, which have a million or so groups, and they in turn may be parts of superclusters, having some ten-thousand clusters.
The Interstellar Medium (ISM)
Experts study the characteristics of whatever floats through interstellar space by observing its interaction with starlight, and they find scattering properties in different colors at different wavelengths. Classical studies have made use of such observations with special instruments such as spectrometers and polarimeters at large telescopes.

Another branch in astronomical science studies molecules that are either drifting freely in space or are attached to interstellar grains. Faint glows emitted by hydrogen molecules sometimes show clouds of interstellar gas. The reason for emphasis on this interstellar medium of gas and dust is that they play a primary role in the formation of the stars. The reason for mentioning the ISM here is that we use it for the study of the inter-universal medium (IUM).
Introduction to Dark Energy and Dark Matter
There is a special challenge in astrophysics and cosmology, which is to understand the physical nature of dark energy and dark matter observed and called by these names, but not understood until now. They are the dominant contents of our universe. You will see the miracle occurring when we switch from our sole universe to considering the multiverse; both problems will then be solved in an elegant manner.
Observable matter, which is called ‘baryonic’, from the Greek word barys, or heavy, accounts for only 4.6 % of the total mass in the universe, while neutrinos equal less than 1 %. The rest is ‘dark’ or not observed: 23 % of dark matter, while 72 % of the total is in some form of dark energy, believed to be the cause of the acceleration of the intergalactic space expansion.
It was not always so. The abundances were not the same when the universe was young as they are now, and that may be a clue for origins. When the universe was young – age 380,000 years – the observable universe was made up of 12 % atoms, 15 % photons, 10 % neutrinos. What was not observable but otherwise derived to be present was 63 % dark matter and a small amount of dark energy.
The Cosmos Has a Single Unified Physics
Young Chandrasekhar showed such promise at the age of 19 at school
in Madras (now Chennai), India, that he was accepted for PhD studies at Cambridge University in England. During his long sea voyage
to Britain,
he did much of his work on stellar
structure, which he would further develop throughout
the 1930s, and for which he would
receive the Nobel Prize in 1983. He moved to the Yerkes Observatory of the University
of Chicago in 1937 and to the Chicago campus in 1956.
His equation for masses I referred to at the start of this paper is
M(α) = (hc/G)a H1–2a, (Eq. 1)
in which h is the Planck constant, c is the velocity of radiation, G is Newton's gravitational constant, and H is the mass of the proton; positive exponents α identify the objects shown in Table 1. The derivation takes seven pages, and there was some awe about it, that Chandrasekhar (1951) was aware of – he did publish the equation four times – but he thought it was too early to use it to explore ‘...deeper relations between atomic theory and cosmogony...’ Shu (1982) referred to it in his classical textbook as ‘...one of the most beautiful and important formulae in all of theoretical astrophysics...’ Max Planck had already expressed the possibility for extraterrestrial application of constant h:
…the possibility is given to establish units for length, mass, time and temperature, which, independent of special bodies or substances, keep their meaning for all times and for all cultures, including extraterrestrial and non-human ones, and which therefore can be called ‘natural measurement units’… (Planck 1899).
He wrote that more than a century before the present time, when we had not as yet discovered any society on a planet of another star. What he probably surmised is that the Cosmos has a single physics that is nearly perfect; it is that physics we consider in the Chandra-Multiverse model.
At the time, however, no one did anything with Chandra's equation. The time was not ripe; one had to wait for large telescopes and powerful spacecraft to deliver essential information about our own universe. This began in 1989 with the Cosmic Background Explorer (COBE) and the Wilkinson Microwave Anisotropy Probe (WMAP) that followed (Spergel et al. 2007).
I started working with Chandra's equation in 2001. The only purpose of the term H1–2a is to
be able to use any unit for the mass, such as kilograms and solar masses. But
these would be useless in a multiverse; other planetary cultures would have
their own units. For a truly universal
mass, the obvious choice of unit is that of the proton. If all masses are
expressed in terms of proton mass
H = 1 and H1–2α = 1 for all values of α, such that:
M(α) = (hc/G)α. (Eq. 2)
It appears to be a concise and powerful combination in terms of the Cosmos' physics, which would encompass perfect versions of quantum, relativity, gravity, and atomic physics (the latter because all masses are expressed in terms of the proton mass, H).
The next excitement was to see what happened for various values of exponent α, and that is in Table 1. Chandra had already published these values for the mass for the ‘primordial stars’ that provide our heavier atomic nuclei (spectral type O) at α = 1.5, and the mass of our universe at α = 2.0. The values under ‘units shown’ were computed with his Eq. 1; s.m. = solar masses. Each step of ∆ α = 0.50 is a factor of 3.3×1019. The last column has observations presented in values of α, for comparison with the first column. It is remarkable that the proton mass, determined in laboratories, would occur in Table 1, alongside the stupendously large structures of the cosmos, all by using the same equation. Observations became the predominant feature of this model, in the end as many as 30 have been used; this is unusual in cosmology.
Table 1. Computed and observed masses
|
Computed α |
Proton mass |
Units shown |
Type of object |
Observed α |
|
2.00 |
1.13×1078 |
9.52×1020 s.m. |
Primordial universe |
1.998–2.008 |
|
1.50 |
3.47×1058 |
29.179 s.m. |
Primordial stars |
1.49–1.53 |
|
0.50 |
3.26×1019 |
5.46×10–8 kg |
Planck mass |
0.500 |
|
0.00 |
1 |
1.67×10–27 kg |
Proton |
0.000 |
At this point, I was not rushing forward, but checking the
quantization and the enormity of its consequences, because this modeling was
clearly going outside of our universe. A correlation with Max Planck was found.
On the last pages
of his classical paper that initiated quantum mechanics, he has a derivation of
units. For mass it is:
M(α) = (hc/G)0.5, (Eq. 3)
which is what we now call the ‘Planck mass’. He found the units from dimensional analysis of the cosmological constants h, c, and G. Chandra's analysis now provides the numerical calibration of the Planck mass. Eq. 3 looks like the Planck mass with a variable exponent; it might be called ‘the universal Planck mass’, and it is used in Table 2, below.
It is easy to do a dimensional analysis as a
trial-and-error until getting a mass; for instance the Planck mass in
kilograms is (m2 kg s–1 m s–1 m–3
kg s2)0.5.
The numerical values of the constants are being improved all the time
(except for c); modern values for it are published yearly by Mohr and Taylor
(2005). In 2005, their numerical values for the constants and their
dimensions were
h = 6.626,0693(11)×10–34 m2 kg s–1, c = 299,792,458 m s–1
(in a vacuum, exact by definition), G = 6.6742(10)×10–11 m3 kg–1 s–2.
The treatment of the present paper indicates that the Planck constant is h, not ħ = h/2π, as is now used in most of the literature; it is easily seen that the values in the Tables would be off unrealistically for ħ. Three of Planck's units are:
Planck mass = (hc/G)0.5 = 5.455,55(40)×10–8 kg, (Eq. 4)
Planck length = (Gh/c3)0.5 = 4.051,31(30)×10–35 m, (Eq. 5)
Planck time = (Gh/c5)0.5 = 1.351,38(10)×10–43 s. (Eq. 6)
The Planck temperature and charge are also considered members of the basic set, and there are derived units; the entire set is called ‘the Planck domain’.
Theoreticians prefer to have quantization in steps of whole units rather than fractions, and Table 2 shows a form of Eq. 3 for statistics with whole numbers for N. The key equation of cosmic masses is then,
M(N) = (hc/G)0.5N, (Eq. 7)
where the exponent gives the values of N shown in Table 2. N = 2 may be for the mass of the planetesimal; this needs checking by an expert. The constant quantization factor of 0.5 in the exponent yields the same factor 3.3×109 as before; for instance, the Local Group has 3.3×1019 universes. Note the arrow pointing up as α is not restricted so that there may be other steps of universes; the quantization topic needs expert study too. A theoretical challenge for future work may be to explain the mechanism of quantization. Such a solution seems to resort to the basic studies of quantum physics, with its connection to Planck's constant h. The cosmos has a quantized distinctness, without which it would be an amorphous brew.
Table 2. Masses in steps of Planck mass
|
No |
Proton mass |
Type of object |
|
5 |
3.7×1097 |
Local Group of universes |
|
4 |
1.1×1078 |
Universe |
|
3 |
3.5×1058 |
Original star |
|
2 |
6.7×1038 |
Planetesimal |
|
1 |
3.3×1019 |
Planck mass |
|
0 |
1 |
Proton |
The numbering of the alphas in M(α) and of N in M(N) is, however, an anthropic curiosity because we think of our universe as having α = 2.00, while another culture in another universe will at first do the same for its own universe. Imagine another culture elsewhere, with its intelligent beings seeing a hierarchy as we do, within and outside of their universe. They also start with their symbols for h, c, G, and H, which are measured in their laboratories, and they consider that their ‘α values’ are from 0 for the proton mass to 2.00 for their ‘universe’, and onward out into ‘the multiverse’. Their universe is then imagined by them as we do for ours, as a member of an assembly of 3.3×1019 universes at α = 2.50, which is a member of 3.3×1019 assemblies at α = 3.00, etc. However, while their universe is at their α = 2.00 and is followed by their 2.50 outside, for us these two may be, for example, at our α = 7.50 and 7.00.
The fact that the equations are open – that α in Eq. 2 and N in Eq. 7 are unrestricted – has brought us the multiverse; I believe that an expert study is needed to establish whether it is an infinite multiverse. In any case, the equations set this multiverse apart from other models in having several characteristics of the universes. To begin with, we know their number at each step, with 3.3×1019 in the Local Group, the next step in the quantization being 3.3×1019 larger, etc. The h, c, G, and H cosmic physics is the same for all; the universes therefore are the same in their grand design, except for age (having started from inter-universal clouds at different times), and perhaps for some small effects of evolution.
This is such an important point that it bears repeating in different words. If our universe resulted from, and is decaying back into the inter-universal medium, the IUM must have the h, c, G, H physics we know for our universe. The IUM has uniformity through mixing of debris from a large number of universes, and they all emerged from the IUM as well, such that all universes surviving from the medium have that same physics.
Another characteristic is the critical mass. ‘Critical’ is defined as being not too large, or the universe would gravitationally collapse under its own weight; and not too small, or lack of gravitational pull would let the universe quickly expand into nothingness. The mass for N = 4 is indeed near that critical mass for our universe, and thereby for all others in the multiverse. Any universe with a mass different from this critical limit would simply not have survived; it would have collapsed or blown apart.
The interaction between the universes is by their expansion. The effect is seen from a bridge over a quiet pond on which raindrops fall. The rings on the water expand and travel through each other. The result in three dimensions is a thorough mixing of the debris from old universes. The resulting new universes will then be the same in composition because the mixing brings material together from many old universes.
The multiverse endowed the universes with their mass, energy, physics, and evolution. Each universe is thereby capable of doing all that we observe in our universe. That may include evolution going as far as having cells and chromosomes for its tools, and making beings who claim to be intelligent as one of its species, depending on local conditions such as the right distance of their planet from the central star. Comet and asteroid impact is also an uncertain factor.
The time scale of the multiverse is estimated by using the scaling factor of the Tables, 1019, times the lifetime of our universe, ~1011; the resulting 1030 seems consistent with the observations of the half-life of the proton. This is probably a real average, as some universes may have longer times, and others shorter, to come to the epoch of their formation through random cloud accretion.
The predominant characteristic of the multiverse is, however, that it is an evolutionary system (Gehrels 2012). It has the abundance of time and possibilities for change, just as Darwin and Wallace's evolutionary model for life had long times and much trial and error. The physics, the forces and components more basic than photons and protons are established and maintained during the long times and through many universe-samples in the multiverse. Universes that do not succeed end back in the inter-universal medium.
This
intense and extensive evolution explains the fine-tuning of the nuclear
transactions in stars that Fred Hoyle used to point out, how the selections and
combinations could not have occurred if the physical constants of the elements
had been even slightly different (Hoyle 1999, originally 1987, is actually on
a discrepancy he had with Darwin's theory). The fine tuning, or any
evolution, could not have happened if ours had been the single Big-Bang universe unfold-
ding fast in the times before t ~10–6
sec, 1037 PT
on the standard clock.
The Aging and Decaying of Our Universe
We now begin a history of our universe, discussing its decay and demise first because we are in that stage at present so that we can identify the components of debris that are spreading into the multiverse. The major concepts of evolution include birth and demise; that we must die is therefore an evolutionary predicament.
Not only people and animals die, but inorganic substances age and
decay as well. Even the protons may have a
limited half-life, predicted at greater than
1050 years, but
they are observed to be at least 1033 years old. This model then becomes useful right away because these two large numbers have been
puzzling in comparison to the lifetime of our universe, which is some 1011
years. Why would the proton have evolved to live that long? The large numbers
now are nicely in perspective with the timescale of the multiverse, ~1030
years.
In summary, our universe is slowly dying with aging stars and galaxies.
The dying of universes is a basic process in evolution, because the debris of
radiation, atomic particles and other masses are used in the accretion for new
universes.
Debris of Photons, Protons and Everything Else
Photons emerge from stars, supernovae, gamma-ray bursters and other energetic sources. Their aging is in terms of moving out, cooling steadily. Their radiation is observed 3,000 K at age 380,000 and 3 K at present. On the time scale of 1030 years, the old photons must be near zero degrees during most of their time in the multiverse. The situation near 0 Kelvin, –273.15 degrees Celsius, ‘absolute zero’, needs to be studied by experts, including the common understanding that all thermal activity stops. I use the term ‘near 0 K’ for what seems to be the ground state of photons, protons, etc.
The protons cool in the expansion as the photons do; other particles such as neutrons and electrons, they all are part of our universe's decay debris, as are old stars and brown dwarfs. Whole galaxies expand outwards too – and clusters of galaxies – while they internally keep their gravitational ensemble together for whatever is aging inside; these mass configurations, as decayed as they are, appear conserved in the multiverse because they are recognized with the Wilkinson Microwave Anisotropy Probe (WMAP) in our early universe. Dark matter and dark energy must be included in the discussions too because they are abundant in our universe, 23 % and 72 %, as we saw above.
The Acceleration of the Expansion
In the late 1990s, two teams of observers went to two different but large telescopes on the prevailing prediction that the expansion of our universe is decelerating, such that a shrinking and collapse would be its fate. Because of their competition and interesting goal, the astronomical world seemed to be travelling with them. The two used the same techniques and made the same opposite discovery: of an accelerating universe as of age 5,000 million years after the beginning, which is at 5×109 years of age for our universe (Goldhaber and Perlmutter 1998; Riess et al. 1998).
The discovery is crucial for the Chandra-Multiverse model because a decelerating expansion, leading towards collapse of our universe, would have made it impossible. We speak of accelerated expansion of intergalactic space, and now see how all the debris of a decaying universe proceeds on the accelerated expansion into the inter-universal medium in which our universe is imbedded.
Furthermore, the cause of the acceleration was interpreted to be dark energy (Riess et al. 1998), and we will use this as the key to the physical interpretation of dark energy below.
The Inter-Universal Medium (IUM)
The description of the IUM uses the extensive knowledge and understanding of the interstellar medium (ISM) between our stars and galaxies. The ISM is tenuous in most places while in others there are extended clouds of hydrogen and other molecules. The ISM clouds have lifetimes of ~109 years, there is always motion in the universe so that they encounter, combine and grow. Concepts from the ISM may be used in this modeling because the same types of processes are bound to happen in the IUM, albeit over much larger cosmological scales of time, ~1030 years. The comparisons must, however, be made with care because the conditions of size, density, radiation environment, etc. of the two media differ greatly.
Anyway, the space density in the IUM will be as uneven as it is in the ISM, with huge clouds accreting. The clouds grow by sweeping the material up during their motion through space. Eventually, self-gravitation will become dominant by its increasing gravitational cross-section, speeding the sweeping and contraction of the cloud towards making a new universe.
The principal difference of the IUM is in its composition, now no longer the young and active material of hydrogen and other atoms but, instead, the above old and cold decayed debris objects that had come long before from dying universes. This is energy seeking material. Gravitational energy of the contracting cloud is now being used internally. The growing proto-universe can therefore increase in mass without getting as hot as a proto-star would do, because the gravitational energy is used to re-energize the old cold photons and to re-energize and re-constitute the atomic particles into regular photons, protons, and neutrons.
That this actually happens is seen in observations of the preservation of characteristics, for instance the clustering of galaxies coming from old universes being recognized for our young universe, as was mentioned above. In other words, the characteristics have not been melted away.
Now we are ready to consider the cloud of the IUM that made our new universe. The spherical gravitational mass is of overall uniform composition because the debris from many universes is mixed together, with all the above components of old photons, subatomic parts of protons and neutrons, and of dark mass and dark energy. This is the uniformity found by the COBE spacecraft till the third decimal of 2,728 K.
Characteristics of Photons
Cooling is the prime characteristic of this decay, and it is here connected with the expansion whereby the density of the material diminishes as a cooling mechanism. We then speak of old cold photons, of old cold protons, etc. COBE discovered them to have 3,000 K at age 380,000 and 3 K at present. At the 1030-years time-scale of the multiverse, they all spend most of their existence near absolute zero. Their ground state is therefore near 0 K; the energy equation of photons has a zero-point energy term (Lamb 1995). Only occasionally may they be scooped up to proto-universal duty, and only a very few will serve the most complex and capable form of evolution known to us as life.
Photons are even more important than the protons because there are at least 109 more of them; this enormous ratio may become better understood with the role the photons play in the birth of universes in the present model. The characteristic most needed here is their radiation pressure. It depends on the fourth power of the temperature, such that it will be strongest for re-energized photons, rather than for the old cold ones.
The Proto-Universe and Photon Burst
We are now ready to pursue the cloud that started our universe, the universe's nebula, towards the more advanced form that is called the proto-universe. We recall that the IUM composition is totally different from that in the ISM, namely of decayed energy-seeking debris. This is the first reason why the growing proto-universe did not become impossibly hot and the galaxy clustering was observed; 1013 K will be its maximum temperature, as the standard models indicate. The mass of our baryon universe is equivalent to 1021 solar masses, but it consisted at this time mainly of energy-absorbing material, and may therefore not have collapsed into a black hole during accretion.
The second reason is the radiation pressure of photons, which provides counter-action to gravity. Imagine a box in IUM space, with radiation from many photons pushing in all directions, but at the periphery of the box the pressure is outward. That results in direction opposite to that of gravity in the proto-universe cloud; it will have negative sign if and where one uses a positive sign for gravity.
It is noted that the maximum temperature of 1013 K makes it unnecessary to do a computer modeling at this time. Before a detailed modeling, an outline like this is needed, so we proceed with the history of our universe on first principles.
The rate of accretion was first controlled by the geometrical cross-section of the cloud, but gradually the larger gravitational cross-section would accelerate it. Already then, the cloud would gain outward force due to radiation pressure. During the accretion this build-up of pressure lagged behind the gravitational force of the cold photons. It brought about the appropriate temperatures, from near 0 to 1013 K, as density increased from the start at ~10–28 to 1018 kg m–3, but that would take time for the heat to penetrate, and cause a delay. The gravity thereby prevailed and the accretion continued.
The fourth-power dependence of the radiation pressure on the temperature must have caught up to end the accretion phase. The remarkable epoch would be reached for the completion of re-energizing the photons, namely at 1018 kg m–3 and 1013 K, at the time of t ~10–6 sec on the old clock at which we know these three conditions from the Standard Model for Big Bang as well as the one for atomic physics.
An increasingly enormous number of old photons reached their full radiation; in other words, an inferno flared out. It must have increased from a small to a maximum central volume; the maximum depends on the total mass and on the percentages below. That central region of sizeable volume was converted from old photons to re-energized radiating photons in a Photon Burst. The one-but-last paragraph of this paper has more information about this stage.
The Photon Burst may have been detected by WMAP as a shell beyond that of the 3-K radiation; i.e. of greater radius than that of the 3-K radiation. Analysis of that WMAP observation would confirm that a flaring occurred like thousands of Super Novae!
Another observation may support this reasoning, in addition to the percentages observed uniformly and of a WMAP verification, namely that we do not observe a center for our universe. This confirms that the enormous Photon Burst brought passage and thereby mixing of baryons with the non-baryons throughout the whole universe. This explains that ‘12 % atoms, 15 % photons, 10 % neutrinos, 63 % dark matter and little dark energy’ were observed by COBE and WMAP everywhere the same in our early universe.
Continuing in the central volume is the re-energizing of the protons etc., which took longer than that of the photons because they were more complicated. They however encapsulated the inferno by holding the photons back through multiple scattering, which sustained the expansion; now the appropriate temperature from 1013 K to 3,000 K was lagging behind the decrease of the density from 1018 to 10–19 kg m–3, because the cooling took time. The multiple scattering thereby prevailed and the expansion continued.
At t = 380,000 years, the space density had become low enough for the electrons, protons and neutrons to combine, to make atoms. Atoms have internal space to let photons pass through them; remember the ‘stadium experiment’ in the beginning parts of this paper. This blast would also have a pressure blowing the IUM material further away from the completed universe. The expansion continued for there was nothing to affect it, until age 5 x 109 y when the acceleration occurred.
The Identity of Dark Energy
We have seen in the previous section that at age 380,000 years there was only a small amount of dark energy left. The dark energy was apparently mostly used up in the accretion and birthing processes and so were most of the old, cold photons. A discovery thereby occurs: dark energy is the energy of old photons; causing the expansion has the same physical action as accelerating the expansion, which was mentioned above as being due to dark energy (Riess et al. 1998). In other words, the conclusion is that the original expansion was caused by dark energy, which also caused the later acceleration.
There appears an indirect but powerful reasoning to confirm this interpretation of dark energy. The evolution in the multiverse could not have left unused the major part of what each decaying universe contributes to the IUM, the old, cold photons (or, in the second interpretation, the 72 % dark energy). They must have been fitted into the evolution of universes and their survival. If they would have been left unused, the ever-increasing number of old-photon debris (i.e. dark energy) would have overwhelmed the cosmos.
The Identity of Dark Matter
The Chandra-Multiverse model might also provide a confirmation of the solution to the problem of the physical nature of dark matter, for which there is already a large literature. Astronomer Bernard Carr (2001) has a critical discussion of both baryonic and non-baryonic dark matter. Physicist Padmanabhan (2002) concludes: ‘both baryonic and non-baryonic dark matter exist in the universe, with non-baryonic being dominant’. His general rule is: ‘There is not an a-priori reason for the dark matter in different objects to be made of the same constituent’. He also discusses baryonic and non-baryonic matter such as protons, WIMPs, axions, neutrinos and massive astrophysical halo objects. Their results support that old, cold protons and other particles, such as neutrons and electrons, are part of our universe's decay debris, as are whole galaxies (each gravitationally holding its debris), clusters of galaxies, and whatever other debris such as old stars. As a short name for all these we use ‘protons, etc’.
The dark-energy actions for multiple scattering and expansion have a counterpart in the dark-matter actions – the one gives and the other receives the kinetic energy of the photon. In other words, while dark energy is the kinetic energy of photons, old or new, dark matter may be the name for the ensemble with which these photons interact, old protons, etc.
This view of dark matter has the same simple but firm confirmation as dark energy. The evolution in the multiverse could not have left unused the major part of what all decaying universes contribute to the IUM, namely their 23 % dark matter (old protons, etc.). If this matter had been unused, the ever-increasing amount of dark matter would have overwhelmed the Cosmos.
The Cosmological Constant
The cosmological constant is sometimes held responsible for the acceleration of expansion at the universe's age of 5×109 years. The previous scenario applies just as well as the cosmological constant for the physical acceleration action by old photons. There is a certain form of logic in it: That the multiverse evolved the properties of the photons, in order to get the cycle of decay and rebirth accomplished, for expansion and survival of the system. In the equations, that is expressed as a cosmological constant.
A refined support of the model appears in the fact that the cosmological constant is exceedingly small, because its theory entails fine-tuning of physics and nature to ‘bizarre’ accuracy (Padmanabhan 2002). Hoyle (1999 [1987]) used similar strong words alike ‘bizarre’ for extreme fine-tuning of the nuclear constants inside stars. The evolution of the universes in the multiverse has indeed bizarre long times: ~1030 years, and numbers of samples, >1019 universes. That is how the Chandra Multiverse accomplishes extreme fine-tuning for all parameters and characteristics of the universes.
Schwarzschild’s Confirmations
In conclusion of this paper is a warning that there was no Big Bang by Schwarzschild (1873–1916), which also confirms the Chandra-Multiverse model. He was a well-known and versatile physicist in Germany who had volunteered for duty during World War I. He caught a serious illness on the Russian Front, but worked on elucidating one of Einstein's equations until the end of his life (Schwarzschild 1916). It included a discussion that can be illustrated as follows.
Light can escape only when its kinetic energy is greater than its potential energy,
GMm RS–1 < ½ mc2, (Eq. 8)
such that there is a limiting radius of the body,
RS > 2GM c–2, (Eq. 9)
which is 3×108
lightyears; that is the radius of our universe at age 380,000 when the
radiation did escape. Table 3 shows the comparison of RS with radius
R = (3M/4πσ)1/3 for a sphere with
uniform space density σ; M = 1.13×1078 proton masses.
The first line applies for the above case when the universe's radiation did escape, R/RS = 1. The Schwarzschild limit does not seem precise because standard theories predict that density to be ~10–19 kg m–3 at that time, not 10–23. However, the precision of these predictions is low and the effect is small, because if 10–19 were used in the calibration of RS, the following ratio is still rounded off to 10–14, and the next is 10–38 instead of 10–40.
Table 3. Radii and Schwarzschild radii
|
R/RS |
t |
σ |
R(ly) |
|
1 |
380,000 y |
10–23 |
108 |
|
10–14 |
10–6 sec |
1018 |
10–5 |
|
10–40 |
0 |
1096 |
10–31 |
The second line is for the above starting time of our universe, t ~ 10–6 sec, using proton density of 1018 kg m–3 to derive R. Because R/RS = 10–14 is so very negative, the Schwarzschild radius indicates a giant black hole, but our entire universe is not a black hole. Furthermore, for photons to escape at age 380,000, they must have been generated much earlier. In the case of the Sun, it takes a million years for a photon generated at its center to escape; physically that is a different situation, but it serves this comparison. The shorter time of 380,000 years may be appropriate, even though the body is much larger than the Sun, because the medium is expanding. The photons' scattered journey was increasingly speeded up because it went through diminishing density, eventually as low as the above 10–19 kg m–3 (which was the density of the whole universe).
In the third line, the Planck density of 1096 kg m–3 is used for obtaining R and thereby R/RS. Under these conditions, the Schwarzschild limit calls resoundingly for a giant black hole of our whole universe. Our universe was not a black hole, and neither radiation pressure nor dark energy is available to save the modeling (this is not to say that our universe would not have smaller black holes, of course). The Table confirms the Chandra-Multiverse model.
Acknowledgements
It is a pleasure to acknowledge the support and suggestions of Kees de Jager, Leonid Ksanfomality, and Barry Rodrigue.
References
Bitbol M. (Ed.) 1995. The Schrödinger Interpretation of Quantum Mechanics. Woodbridge: OxBow Press.
Carr B. J. 2001. Baryonic and Non-baryonic Dark Matter. Birth and Evolution of the Universe / Ed. by K. Sato, and M. Kawasaki, pp. 55–70. Tokyo: Universal Academy Press (earlier version at URL: http://arxiv.org/abs/gr-qc/0008005).
Chandrasekhar S. 1951. The Structure, the Composition, and the Source of Energy of the Stars. Astrophysics, a Topical Symposium / Ed. by J. A. Hynek, pp. 508–681. New York: McGraw-Hill.
Everett H. III 1971. The Theory of the Universal Wave Function. The Many-Worlds Interpretation of Quantum Mechanics / Ed. by B. S. DeWitt, and N. Graham, pp. 3–140. Princeton: Princeton University Press.
Gehrels T. 2011. Can We Do without the Big Bang? Tucson, AZ: University of Arizona BookStores..
Gehrels T. 2012. Survival through Evolution, from Multiverse to Modern Society. 2nd ed. Tucson, AZ: University of Arizona BookStores.
Goldhaber G., and Perlmutter S. 1998. A Study of 42 Type Ia Supernovae and a Resulting Measurement of Omega(M) and Omega(Lambda). Phys. Letters 307(1–4): 325–331.
Greene B. 1999. The Elegant Universe, Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. New York: Random House.
Hoyle F. 1999[1987]. Mathematics of Evolution. Memphis, TN: Acorn Enterprises.
Lamb W. E. Jr. 1995. Anti-Photon. Applied Physics B 60: 77–84.
Mohr P. J., and Taylor B. N. 2005. CODATA Recommended Values of the Fundamental Physical Constants. Reviews of Modern Physics 80: 377–470, Table XXVI.
Padmanabhan T. 2002. Theoretical Astrophysics. Vol. 3. Galaxies and Cosmology. Cambridge: Cambridge University Press.
Planck M. 1899. Über irreversible Strahlungsvorgänge. Sitzungsber. preusz. Akad. Wissenschaften 5: 440–490.
Randall L. 2005. Warped Passages. New York: Harper-Collins.
Randall L. 2007. The Case for Extra Dimensions. Physics Today 60(7): 80–81.
Riess A. G. et al. 1998. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 116: 1009–1038.
Schwarzschild K. 1916. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitzungsberichte Königlich. Preus, Akad. Wiss. Berlin, Phys.-Math. Klasse 189: 189–196; translated in 2003, On the Gravitational Field of a Mass Point according to Einstein's Theory. Gen. Rel. Grav. 35(5): 951–959.
Shu F. H. 1982. The Physical Universe. Mill Valley: University Science Books.
Smolin L. 2007. The Trouble with Physics. New York: Houghton Mifflin Co.
Spergel D. N. et al. 2007. Wilkinson Microwave Anisotropy Probe (WMAP) Three-Year Results: Implications for Cosmology. Astrophys. J. Suppl. 170(2): 377–470.
Steinhardt P. J. 2011. The Inflation Debate. Scientific American 304(4): 36–43.
Steinhardt P. J., and Turok N. 2007. Endless Universe, Beyond the Big Bang. New York: Doubleday.
Vilenkin A. 2006. Many Worlds in One, the Search for Other Universes. New York: Hill and Wang.
Woit P. 2006. Not even Wrong, the Failure of String Theory and the Search for Unity in Physical Law. New York: Basic Books.
[1] This notion is explained further in this article.
[2] URL: www.lpl.arizona.edu/faculty/gehrels2.html.
