The Pattern of Agrarian Civilization Survivorship and Its Consequences
Almanac: Evolution:Complexity in Nature, Society, and Cognition
DOI: https://doi.org/10.30884/978-5-7057-6261-3_06
Abstract
Using the data of Kemp, agrarian civilizations are considered as members of a single cohort and their pattern of survivorship is derived fr om these data. Models of survivorship fr om the disciplines of demography and population biology are used as standards of comparison, and it is shown that civilizations represented in this data set exhibit a Type II survivorship pattern. This result is then briefly compared with the work of Sandberg (2023) who demonstrated that civilizations per se do not age. The consequences of these parallel results are then investigated, and the implications of these results are considered within the context of the early 21st century and humanity's future in this century.
Keywords: Type II survivorship, civilization, complex adaptive system, the Red Queen.
Introduction
That civilizations originate, exist in some form for a period of time, and then either expire slowly or collapse is an unstartling statement; archeology is replete with such evidence. Rome, at least the Classic Maya of the tropical lowlands of the southern Peten, the Inca, and the Khmer polities of Angkor Wat and Angkor Thom all collapsed, while the position of France, once the dominant power in Europe, now occupies a reduced position on the world stage, as do the Dutch and British; their reduced prominence a consequence of a much slower process of decline than, say, of the Inca. In general, polities have a lifespan, some of them longer than others, but most can be perceived of as having an origin, a relatively stable middle, and an ending; this is a clear model of historical narrative. Previous civilizations, at least fr om the perspective of temporal depth, can be considered to have (relatively) discrete lifespans and may be considered for their discreteness as single entities. It follows that multiple civilizations can be considered collectively as populations of entities of varying lengths of existence, that is as cohorts. The concept of survivorship as it is understood in population ecology may then be a useful one to apply to the analysis of human civilizations.
Survivorship as a concept has been a useful tool in population ecology, human demography, and a number of related fields for quite some time, in fact several decades. This concept may be best described by considering a cohort of conspecific individuals synchronously beginning their existence and being monitored over time until the last individual expires; empirical lab studies may begin with a thousand fruit flies or some other organism of interest and follow the cohort until the last individual is gone. A graph may then be constructed in which the Y-axis represents by some measure the number of individuals remaining in the cohort, for example at t = 0 the cohort will have its maximum number and there afterwards will be reduced by the number of individuals expired until, at the final time, there are no more individuals remaining. By graphing the log-transformed values of cohort size, a method preferred by demographers in general, per time, a survivorship curve can be generated. It turns out that, broadly speaking, there are three modes of survivorship, and these three different styles of dying have been given the labels: Type I, Type II, and Type III survivorship patterns (see Fig. 1). Please note here that the general forms of each of the types of survivorship are a result of their underlying biology. Type I organisms have low juvenile rates of mortality, Type II organisms die at a rate that is independent of age, and Type III organisms have very high juvenile mortality but much lower adult mortality. Interestingly with respect to Types I and III, mature and aging adults expire at a rate opposite to juveniles; that is to say that aging Type I individuals have a low probability of continued survivorship, while Type III senior citizens have an increased probability of survivorship.
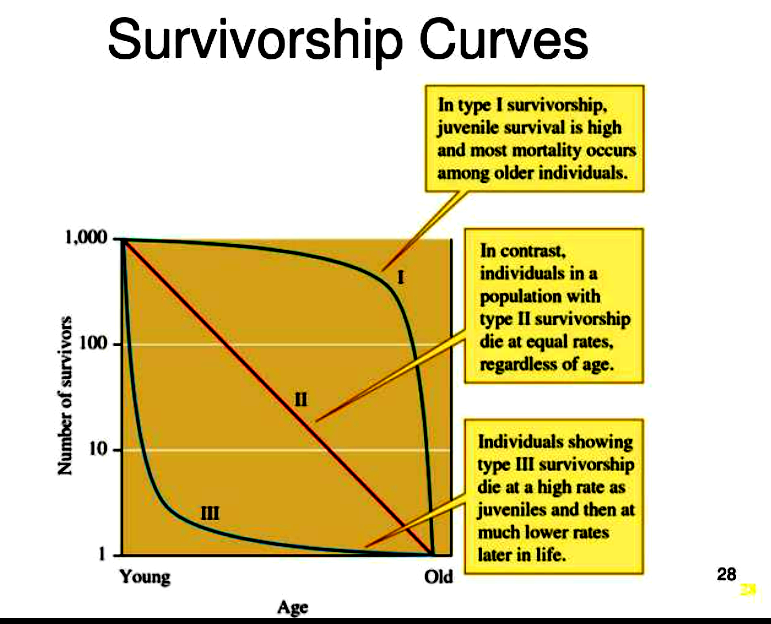
Fig. 1. Survivorship curves
It has also become the habit of population ecologists to label Type III species as r-species and Type I species as K-species, taking the labels fr om the Verhulst logistic equation as follows: dN/dt = rN(1 – N/K), where r = growth rate, N = population size, and K = carrying capacity, i.e. some upper lim it above which sustained existence of a given population is impossible. K-species have high rates of survivorship (at least to reproductive maturity) and low rates of reproduction, while r-species are the reverse, having high rates of reproduction and low rates of survivorship. Pertinence to this paper requires that one further point needs to be emphasized about these demographic distinctions. That Type I individuals have a reduced probability of continued survivorship in old age when applied to a cohort of civilizations would then seem to imply, if and only if civilizations exhibit Type I survivorship, that aging civilizations have a low probability of continuing their existence. It should also be noted that Type III survivorship implies the reverse, a high rate of extinction in the early years of civilization evolution and also that once civilizations have achieved a given age, their probability of continuing to survive is quite high. Examples of Type I, II, and III survivorship patterns are respectively: humans, house sparrows, and clams. Our species has a reduced infant mortality and in fact reduced mortality up to late middle age with respect to western civilization and then a relatively rapid decline, so that mean survival is on the order of 80 years, but continued survival declines rapidly so that relatively few survive beyond the age of 80 and even fewer survive beyond the age of 100. House sparrows live a couple of years at most, but during that time experience mortality is independent of their age; there are then no geriatric sparrows. Type III species have the unenviable quality of having massive infant mortality, just imagine here a clam shedding hundreds of thousands of eggs into the surrounding water with the probability of survivorship to reproductive maturity of any particular egg as proportional to the inverse of the total number of eggs shed; i.e. it is actually zero! However, once survival past a given reproductive age occurs, then continued survival has a much greater probability of continued survival than do the eggs and early stages of clam life. (Please note that these three modes of survivorship are dependent on the interplay between reproduction, length of development, degree of care for young, and adult survivorship; a topic of only ancillary importance here. Also note that the basic population biology discussed here can be found in any respectable text on this subject. Three are listed here: Gotelli [2008], Hutchinson [1978], and Wilson and Bossert [1971]).
More generally, the concept of survivorship may be applied to complex adaptive systems (CAS) en masse. The broader understanding of CAS may include businesses, ecosystems, and civilizations. It is this last category that is the focus of the research reported on here. If a collection of different civilization lifespans can be accumulated and if those civilizations existed under relatively similar conditions, say, of energy acquisition, then this collection of civilizations may be considered as a cohort and the fiction of those civilizations originating at the same time may be indulged in. Therefore, this dataset of civilizations may be treated in the same way as a cohort of individuals and their survivorship can be represented graphically. There is however a significant point of departure with respect to the biology of the survivorship of a relatively discrete biological entity as opposed to a business, an ecosystem, or a civilization; that is the mode of reproduction. At the level of a more dispersed system, the individual units reproduce, but the system itself provides context for that reproduction. The specific processes for graphical preparation will be discussed in the next section.
Luke Kemp (2019) has published lifespan data for ancient civilizations. The time over which the data were collected extends from 3000 BCE to 1000 CE, a period of time over which there were only agrarian civilizations; this implies a similar energy source for all civilizations represented, although surpluses of this energy source used may vary in magnitude. It is important to note that urban area formation is directly associated with civilization existence and therefore with agrarian surplus generated. However, not all civilizations of the time period being considered had significant urban areas; steppe nomads fall into this last category. Even so, the steppe nomad civilizations did depend on civilizations that were urbanized.
A comment should be made at this point regarding the relationship between the magnitude of energy accessible to a given civilization and the degree of urbanization associated with that particular civilization. The pattern of urbanization over the last 5,000 years has been investigated by Harper (2019) as represented by the size of the maximum urban area for the world-system as a whole, that is the globe in toto, over that period of time. This maximum urban area pattern of sizes (with respect to population) over this period of time is punctuated in form revealing periods of stasis separated by periods of rapid maximum urban area growth. It is the contention here that these maximum urban area magnitudes are a consequence of the limits to energy availability, and, as these sizes are characteristic of the entire world-system, they apply to all civilizations extant at a given time. Therefore, individual civilizational characteristics, while indicative of a given civilization, are not determinants per se of maximum urban area limits; those limits are most probably characteristic of the underlying biology of Homo sapiens.
If the level of accessible energy is characteristic of a global maximum urban area magnitude, then the range of change over this 4,000-year period is worth considering; it is by a factor of 30 that the maximum urban areas change. However, over the majority of the time this urban magnitude is stable or oscillates around a mean value, the implication being that energy access over periods of urban area stasis is relatively constant as well, that is the same mechanisms of energy access are in play for the duration of the period of stasis. The pattern itself may best be described as one of punctuated equilibrium, which was first recognized as a pattern representing speciation revealed in the fossil record. This pattern has been identified empirically regarding the evolution of size in maximum urban area populations as well as in a rudimentary way by a math model.
The primary focus of this paper will be the relationship between civilization survivorship, on the one hand, and the punctuated evolutionary pattern of maximum urban area populations, on the other.
Methods
The data of Kemp are organized to show the durations of 87 agrarian civilizations. In turn, these data will first be presented in an order-rank distribution and then from that order-rank distribution and then a size frequency distribution reflecting survivorship will be derived from this distribution, since it is assumed that all 87 civilizations will be a single cohort which begins its existence at the same point in time. Further, as is common practice in this sort of demographic analysis, the Y-axis data will be natural-log-transformed. The sciences of demography and population biology recognize three different survivorship patterns: Type I, Type II, and Type III survivorship patterns (see Fig. 1). It is noted here that Type II survivorship represents constant decay of the original cohort size.
Results
Fig. 2 shows all 87 points from order 1 with a duration of 1,150 years to order 87 with a duration of 14 years. On casual inspection, this distribution has the appearance of an exponential decay, and the equation modelling this pattern is as follows: Nt = Noe–rt. However, a closer look reveals that a clear break separating the first 12 points from the remaining 75 points (see Figs 2 and 3). Both sets of points show a slightly better linear fit than a first order decay fit, while the reverse is true for the entire cohort.
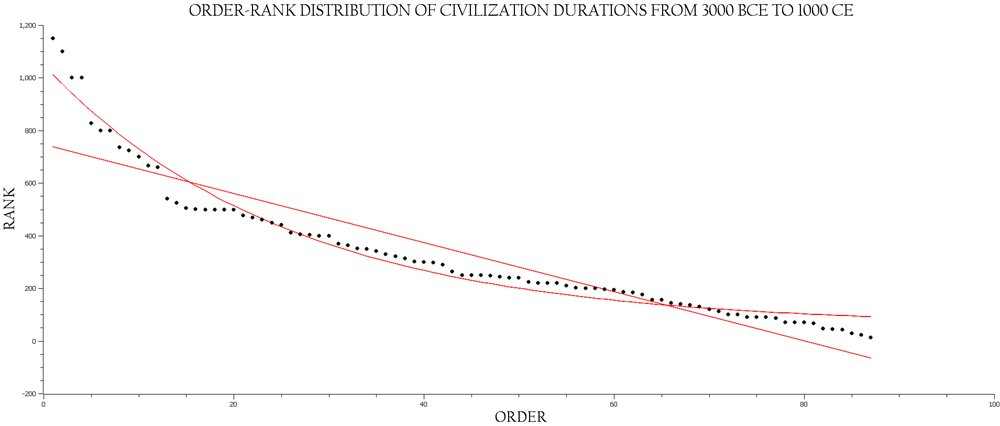
Fig. 2. The clear non-linear distribution of this data
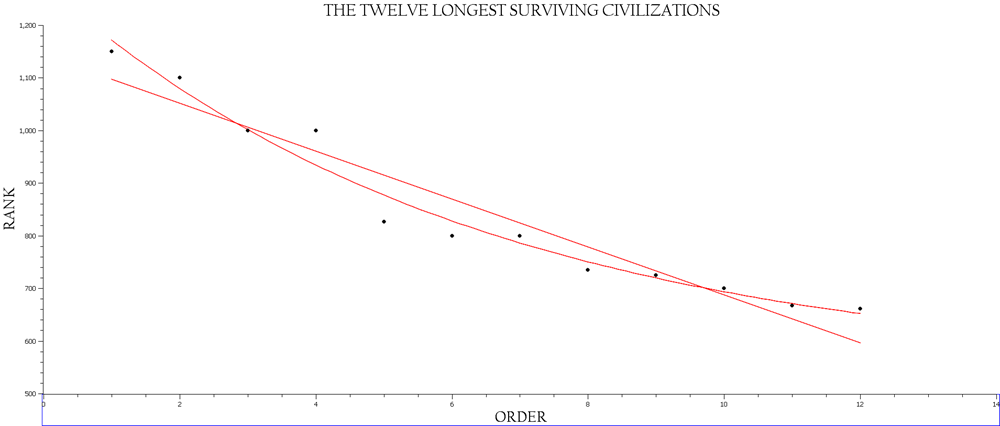
Fig. 3. The near linearity of a plot of the first twelve order-rank points
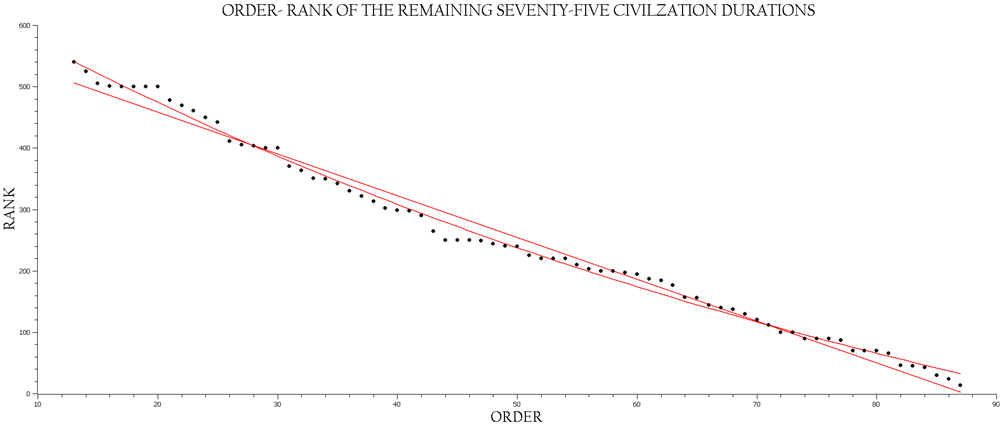
Fig. 4. Order-rank of the remaining 75 civilization durations. The remaining 75 order-rank points also exhibit a near linear distribution
Note: the slopes of this linear regression and the previous one are different with the greater negative slope being attributed to this particular distribution.
When the order-rank data are reorganized into a survivorship size-frequency distribution by taking subsets of the data and the number of durations above some predetermined data point and proceeding at regular intervals, say, durations of 1,000 years, 900 years, and so forth until the entire data set has been subdivided. The order categories will then constitute the X-axis, and the frequencies per division, the Y-axis. A plot of this data (see Fig. 4) reveals another decay curve and can be modeled by the exponential function: Y = 106.6871e–.0035X. The natural-log-transform of this equation gives lnY = 4.6699 – .0035X, wh ere Y is the number of remaining civilizations at a given time, and X represents time (see Fig. 5). This latter equation is that of a straight line, and this form of the equation implies a Type II survivorship pattern and that the risk of extinction is constant throughout the existence of a given civilization. Two aspects of a constant risk of extinction are immediately apparent. First, civilizations do not age. This was pointed out by Sandberg (2023), and the significance of his research in line with the data reported on here will be treated briefly. Second, since risk of extinction is constant throughout the existence of any civilization, those civilizations, any civilizations, are put under conditions of the Red Queen, a character from Lewis Carroll's Through the Looking Glass (2015[1872]), but coopted by the late Leigh Van Valen as a metaphor for the cost of existence. The evolutionary landscape under the feet of any civilization is always moving. Consequently, any civilization, any CAS (complex adaptive systems), must exert a certain amount of energy to adapt and adjust to ongoing change, both internal and external.
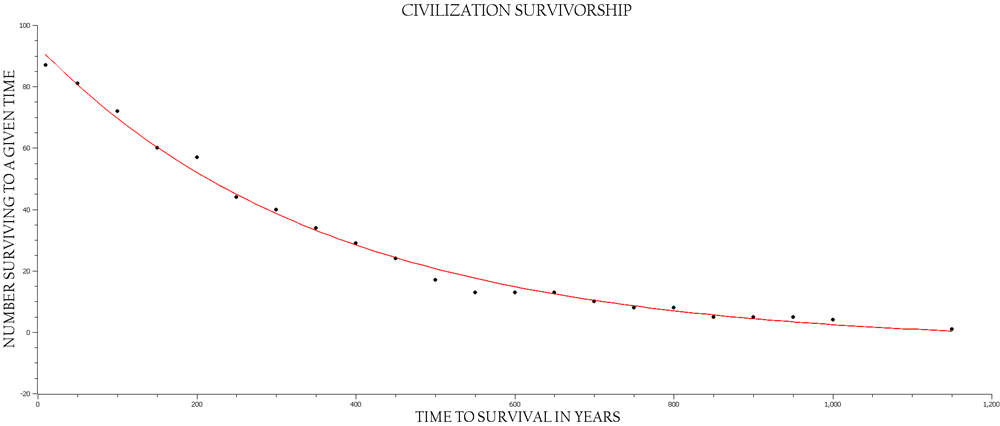
Fig. 5. The size-frequency survivorship pattern of the order-rank data
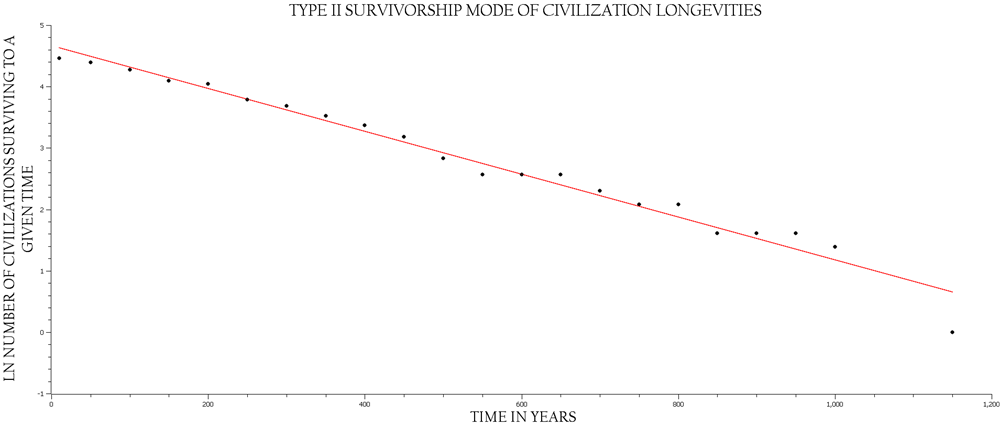
Fig. 6. The natural-log-transform of Y-axis data showing the clear linearity of this set of points
Note: the final point is an outlier.
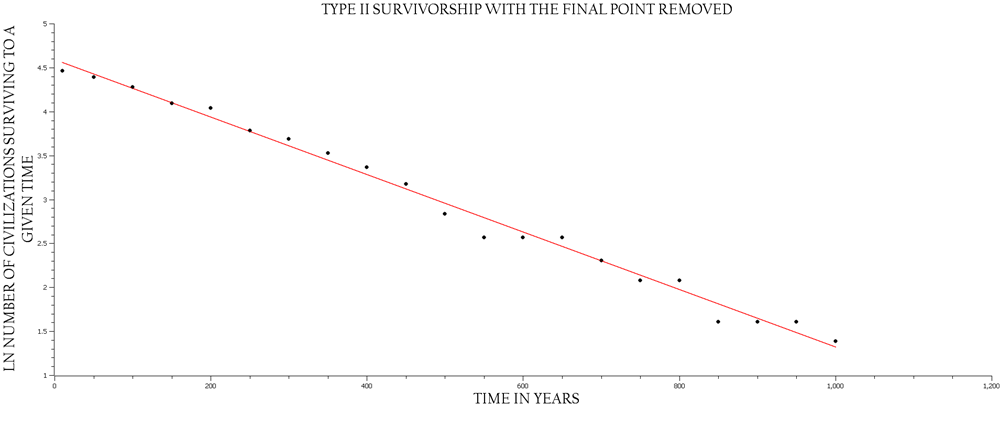
Fig. 7. Removal of the outlier point showing an even better fit for this log-linear plot
Discussion
What are the consequences of the previous results, i.e. that a Type II survivorship pattern is exhibited by agrarian civilizations as represented by the data of Kemp (2019)? From an ecological perspective, the implications are clear; given a starting cohort of a particular size, in the case of Kemp's data, N = 87, this cohort will decrease at a constant rate until the entire cohort is extinguished. [Note that this constancy of decline is best visualized by natural log transforming the Y-axis data giving a linear distribution as represented in Figs 6 and 7.] Type II survivorship is identical to the model for radioactive decay, Nt = Noe–rt, in which the log-transformation of the equation is ln Nt = ln No – rt, and some valuable information may be extracted from this parallel model. First, the rate of change is clearly constant, –r, second, the ratio: ln[Nt/ No] = –rt, so ln[N1/No] = –r, and in turn, N1/No = e–r. This mild algebraic reasoning is given to point out that while with respect to demography R = er, wh ere R represents the rate of replacement, in the case of Type II survivorship this ratio represented by R is decreasing and from time-point to adjacent time-point is constant, i.e. N1/No = N2/N1 and so forth. Further, since N1 = RNo, then Nt = RtNo. For a final point of note, the half-life of civilizations exhibiting a Type II survivorship pattern, t.5 = ln2/r; in the case of Kemp's data, t.5 = .8169, not a particularly long half-life even given that the time units are centuries, i.e. half-life ~ 82 years. If we now briefly step away from the restricted view of survivorship, as informative as this view can be, and consider the larger context of sustainability, it becomes quite clear that reproductive effort must, on average, balance the loss due to the declining rate of survivorship. At the level of organization of a civilization, reproductive effort can only be measured indirectly with respect to its areal size, population size, or economic magnitude. There is only an analogue of reproduction at the civilization level of organization when compared to the reproductive mechanisms of, say, a leopard frog, a chicken, an oak tree...
While the initial portion of this discussion adopted an ecological perspective, a human-historical perspective is the actual context of this paper. As mentioned previously, the negative rate of change, –r, was determined to be r = .0035. This implies that civilizations as individual entities have a .35 % chance of extinction from time unit to time unit, years in this case. It should be noted that civilizations are considered to be neutral units of focus, i.e. they are not considered to be of any specific culture, religion, political bent, or economic focus. This said then implies that some over-riding factor must control civilizational behavior considering the neutral way in which civilizations are treated as units of research. That over-riding factor is energy; the type of energy and the access to that energy will then determine civilization extent and complexity but not survivorship per se. The Type II survivorship mode implies that at a given energy level as reflected by the aforementioned area size, complexity, etc. energy level will be neutral to civilizational loss. This also alludes to the possibility that civilizations do not age (Sandberg 2023), a topic that will be treated next.
There are many theories, either specifically focused, for example the Gibbon's The History of the Decline and Fall of the Roman Empire, or of a more general nature, for example Tainter's The Collapse of Complex Societies, that address the causes and mechanisms of civilizational collapse. To do so they also (may) invoke the notion of civilizational aging. Let us first define aging as a loss of function due to mounting age. This, of course, implies that vulnerability to collapse also increases with age; older civilizations die. Possibly so. In fact, civilizations may change over time, but this does not imply loss of function. Further, disturbances of all sorts may occur to any given civilization, both internally and externally, resetting the clock on that given civilization and perhaps reducing function for a while and also probably changing the trajectory of that civilization, but again these are not examples of aging. Stuff happens! In support of the non-aging of civilizations I would like to consider the work of Sandberg (2023) who discovered that civilizations, defined by him as complex adaptive systems (CAS), do not age, but due to the consequences of system evolution, the risk of CAS demise becomes a consequence of the niche that the CAS finds itself and may increase with time. Since CASs either by design or default are niche constructors, that is the evolution of a CAS affects the environment of that CAS and as a consequence creates a niche that imposes new selection pressures that are feeding backward on the CAS in question, those constructed niches constitute a source of emergent and novel selection pressures; niche construction is an active if unpredictable source of CAS disruption along with the passive source of disruption that is simply being in any particular environment.
It is worth commenting briefly here on the fact that Type II survivorship and its consequences imply that any civilization exists on shifting sands and that those shifting sands constitute a reason to exert energy simply to be aware of the potential for disruption, with the risk of that disruption being constant over time; there is no respite from the risk of civilization downturn. Civilizations then are in the position of the Red Queen. The Red Queen informed Alice that if she wished to go anywhere that wish would have to be translated into greater effort as the continuous movement of the ground beneath her feet required energetic output simply to maintain her position. The further implication for all niche-constructing CASs, among them civilizations, is that they are subject to extinction at any time during their existence.
Some, in fact much, of my previous research has been involved with the study of patterns of urbanization over historic time. That research program has revealed among other things that the pattern of maximum urban area size, Cmax, since 3000 BCE actually consists of two subpatterns, periods of stasis, periods when Cmax remained constant or oscillated about some mean, and periods of punctuated growth in which Cmax continuously increased from some base value. An example of stasis would be the period of time from 100 BCE to 1800 CE in which the mean value of Cmax was approximately 1E6, even though there was considerable oscillation from 100 BCE to 1300 CE followed by 500 years of near constancy at that 1E6 value. An example of punctuated growth would be the 700 years leading up to 100 BCE when the size of Cmax changed from 1E5 to 1E6, a factor of 10X increase. The worlds of stasis and punctuation were different from one another, especially if one realizes that the magnitude of Cmax may be considered as an energy lim it established both as a consequence of the type of energy available and a consequence of the access to that energy. In addition, the distribution of urban area sizes below that of Cmax was different. During periods of stasis those lower levels ‘filled in’ while during periods of punctuation it is the top level, Cmax, that increased in size. This brief tour into urbanization patterns over time was made because if civilization survivorship is in fact Type II, then those different patterns of urbanization should have no effect on civilization survivorship. This research has yet to be done, but I feel it is a legitimate scientific pursuit.
We are entering a time in the early years of the 21st century when disruptive events, potentially civilizational disrupting events, have become part-and-parcel of our existence. A pandemic, multiple ‘small’ wars, a recession, emergent events such as the baby formula shortage and the Southwest Airlines debacle are just the beginning to this century's problems. Xu et al. (2020) have predicted that the climate-change-induced global warming will dislodge at least 1E9 and possibly as many as 3E9 people. In light of the fact that the United States has a border problem of anywhere from a few thousand to possibly a few tens of thousands of ‘illegal’ migrants, hundreds of millions of desperate migrants knocking on the metaphorical American door that is our southern border will make our current problems pale in comparison. I bring these events into focus, because of their magnitude, their occurring globally or at least having a cascading global effect. The world-system as a whole has never collapsed, but like any other CAS has the potential to do so and independently of age. Even though we exist at a different energy level than do agrarian civilizations, if it is concluded that civilizations in general exhibit Type II survivorship, then we face the responsibility of being far more vigilant at the world-system level of (human) organization that we at present are.
References
Carroll L. 2015[1872]. Through The Looking-Glass. Delhi Open Books.Gotelli N. 2008. A Primer of Ecology. New York: Sinauer Associates – Oxford University Press.
Harper A. 2019. The Punctuated Equilibrium Macropattern of World System Urbanization and the Factors that Give Rise to That Macropattern. History and Mathematics: Big History Aspects / Ed. by L. Grinin, and A. Korotayev, pp. 303–339. Volgograd: ‘Uchitel’ Publishing House.
Hutchinson G. 1978. An Introduction to Population Ecology. New Haven, CT: Yale University Press.
Kemp L. 2019. Are We on the Road to Civilization Collapse? BBC Future. URL: https:// www.bbc.com/future/article/20190218-are-we-on-the-road-to-civilisation-collapse.
Sandberg A. 2023. The Lifespan of Civilizations: Do Societies ‘Age’, or is Collapse Just Bad Luck? How Worlds Collapse: What History, Systems, and Complexity Can Teach Us about Our Modern World and Fragile Future / Ed. by M. Centeno, P. Callahan, P. Larcey, and T. Patterson, pp. 375–396. New York: Routledge.
Van Valen L. 1973. A New Evolutionary Law. Evolutionary Theory 1: 1–30.
Wilson E., and Bossert W. 1971. A Primer in Population Biology. New York: Sinauer Associates.
Xu C., Kohler T., Lenton T., and Scheffer M. 2020. Future of the Human Climate Niche. PNAS 117(21): 11350–11355.
