Mathematical Model of Interaction between Civilization Center and Tribal Periphery: An Analysis

Authors: Korotayev, Andrey; Grinin, Leonid; Grinin, Anton L.
Journal: Social Evolution & History. Volume 21, Number 1 / March 2022

DOI: https://doi.org/10.30884/seh/2022.01.03

This article offers an analysis of a mathematical model of the influence of one of the major factors of the World System’s macrodynamics throughout most of its history (since the ‘urban revolution’) – civilizations’ interaction with their tribal peripheries (described in our previous article). The proposed mathematical model is intended to describe the possible influence of interaction between the civilizational core of the World System and its tribal periphery on the formation of the specific curve of world urbanization dynamics. It simulates completion of the phase transition, the behavior of the system in the attraction basin, and the beginning of the phase transition to the attraction basin of the new attractor. The aim is to identify the role of interaction between the civilizational core and tribal periphery in the formation of an attractor effect during the completion of phase transition – that is, to clarify not only why there a slowdown in growth rates of the main indicators of World System development observed following completion of phase transitions during its development, but why these rates fell, with a subsequent temporary stabilization near some equilibrium level. Achievements of modern studies of tribal peripheries, including our understanding of complexity of the tribal periphery itself and its heterogeneity, are considered. The basic principle of the proposed dynamic model is that the size, power and level of complexity in realization of external policy functions in nomadic / ‘barbarian’ unions (empires) closely correspond to the size, power and level of political culture and activity of the core states with which tribal systems constantly had to interact (a point previously established by experts in nomadic studies). Various alternatives are shown in the model. Depending on the power and size of one of the two components of the ‘civilization–tribal periphery’ system, the other component also changes significantly as it has to respond to the challenge properly, or can make less efforts without feeling threat or resistance. This principle is observed throughout the long history of the World System. We show that interaction between the civilizational center and tribal periphery can explain some characteristic features of World System dynamics in the 4^th millennium BCE – 2^nd millennium CE. The patterns of interaction between the periphery and the center of the World System may be useful in understanding current phenomena, such as the migrant crisis of 2015 in Europe.

Keywords: world history, dynamic modeling, the World System, civilizations, tribal periphery, urbanization, asabiyyah, technology, warfare.

Andrey V. Korotayev, HSE University and Lomonosov Moscow State University, Moscow more

Leonid E. Grinin, HSE University and Institute of Oriental Studies, Russian Academy of Sciences, Moscow more

Anton L. Grinin, Lomonosov Moscow State University more

In our previous article (Korotayev, Grinin 2021) we have described a mathematical model of the influence of one of the major factors of the World System's macrodynamics throughout most of its history (since the ‘urban revolution’) – of the civilizations' interaction with their tribal peripheries. The proposed mathematical model is intended to describe the possible influence of interaction between the civilizational core of the World System and its tribal periphery on the formation of the specific curve of the world urbanization dynamics. It simulates completion of the phase transition, the behavior of the system in the attraction basin, and the beginning of the phase transition to the attraction basin of the new attractor. The aim is to identify the role of interaction between the civilizational core and tribal periphery in the formation of an attractor effect during the completion of phase transition – that is, to clarify not only why a slowdown in growth rates of the main indicators of World System development was observed following the completion of phase transitions during its development, but why these rates fell, with a subsequent temporary stabilization near some equilibrium level. The basic principle of the proposed dynamic model is that the size, power and level of complexity in realization of external policy functions in nomadic / ‘barbarian’ unions (empires) closely correspond to the size, power and level of political culture and activity of the core states with which tribal systems constantly had to interact (a point previously established by experts in nomadic studies).

Below we present an analysis of this model.

Typical dynamics generated by the model with average values of parameters and initial conditions are presented in Figures 1–3.

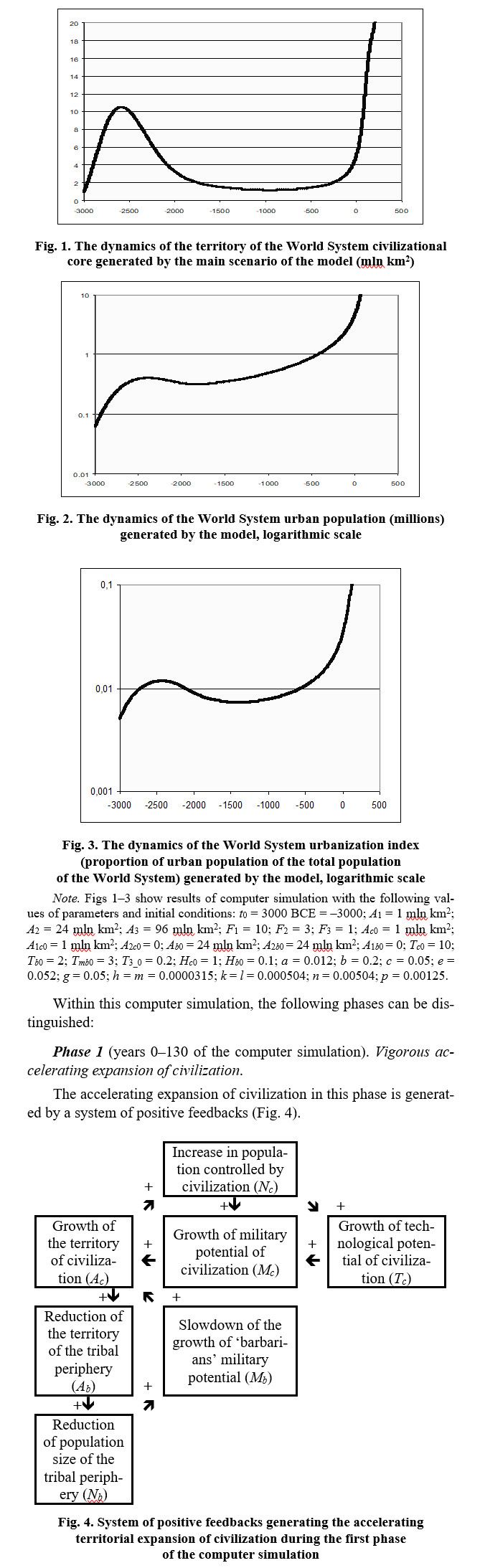
Thus, at this phase the growth of the civilization territory leads to an increase in its population, which results in increase in its military potential both directly (the size of the army increases along with the increase in population size), and through acceleration of technological growth rates (allowing soldiers to be supplied with more effective weapons). The increase in military potential of civilization leads to a further increase in its territory, which results in further acceleration of growth of its population, etc.; on the other hand, acceleration of the growth of the territory of civilization leads to a substantial reduction of the territory of tribal periphery and consequently, a decrease in population size and the military potential of ‘barbarians’ that promotes further acceleration of growth of the territory of civilization, reduction of the territory of the tribal periphery, etc.

At this phase, one can observe the accelerated growth of population of the World System¹, the World System urbanization index² and the urban population.³

Phase 2 (years 130–340 of the simulation). Slowdown of expansion of civilization.

The following system of negative feedbacks comes to the foreground during this phase: the growth of the civilization territory leads to the growth of asabiyyah of ‘barbarians’, which is expressed in increase in the level of their political culture and organization, and leads to the growth of their military potential both directly and through the acceleration of rates of borrowing of military technologies of civilization (including military and organizational and tactical innovations) which results in reduction of rates of growth of the civilization territory which, until it slows down to zero level, continues to lead (through the mechanisms mentioned above) to the growth of barbarians' military potential and further slowdown of rates of territorial expansion of civilization (see Fig. 5).

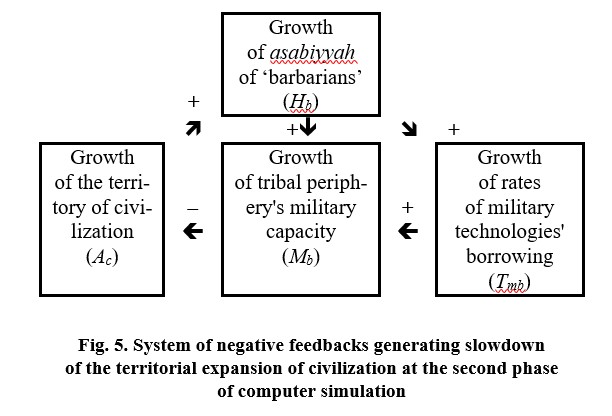
Nevertheless, at this phase the expansion of civilization proceeds at a rather rapid (though less and less rapid over time) rate; a rather rapid (though also slowing) growth of population of the World System also continues. However, since year 154 of our computer simulation, the absolute growth rates of population of the World System begin to decrease, but up to the end of Phase 2, they remain rather high. Starting from the year 209 of the computer simulation the absolute growth rates of urban population also begin to decrease (remaining nevertheless rather high). During this phase, the growth rates of the World System urbanization index decrease almost two-fold (though remaining rather high compared with the subsequent two phases).

Phase 3 (years 340–510 of the simulation). Expansion of civilization is exhausted and stops. Approximate power balance. Tribal periphery begins its counterattack.

During this phase, the territory of civilization in comparison to the territory of its tribal periphery changes rather slowly, no more than 0.01 million km² per year (reaching at the inflection point in year 408 of the simulation, 48 km² per year). At the first stage of this phase, the action of the mechanism of negative feedback mentioned above comes to its logical conclusion – the military potentials of civilization and the tribal periphery become equal, and the rates of expansion of civilization are reduced to zero. However, the process of rather fast borrowing by the ‘barbarians’ of military technologies of civilization continues. As a result, the military potential of the tribal periphery begins to exceed that of civilization, and ‘barbarians’ start their counterattack. At first, it develops extremely slowly (83 km² during the first year); but the beginning of ‘tribal counterattack’ leads to the formation of the system of positive feedbacks giving more and more noticeable results every year – acceleration of the growth of the territory of the tribal periphery leads to the acceleration of the growth of its population, which in turn, leads to an increase in the military potential of ‘barbarians’ and even greater increase in the territory of tribal periphery and consequently, to a greater increase in the ‘barbarian’ population, etc. On the other hand, the acceleration of growth of the territory of the tribal periphery leads to a substantial reduction in the territory of civilization, and consequently, to a decrease of its population and military potential, which promotes further acceleration of the growth of the territory of tribal periphery, reduction of the territory of civilization, etc. (Fig. 6).

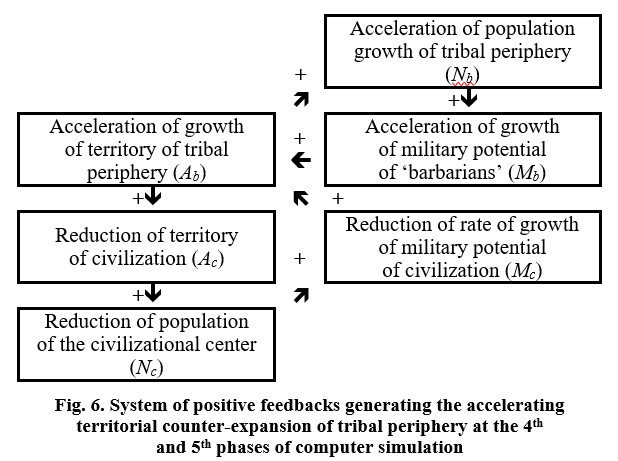
It is remarkable that in our computer simulation by the start of the counterattack of tribal periphery, the total number of ‘barbarians’ (7.9 million) is almost three times less than the number of ‘the civilized population’ (23.4 million), and the index of their general technological development (3.7) is much lower than the level of technological development of civilization (12.1). The counterattack of ‘barbarians’ appears to be possible, firstly, due to a higher military participation ratio peculiar to them; secondly, because at the beginning of the counterattack, their asabiyyah is higher than that of civilization, and, thirdly, because their military technology is much higher (7.15) than the general level of their technological development (3.7).

The growth rates of the total population of the World System decrease almost threefold in this phase, from a moderate 0.125 to 0.043 per cent per year. At the end of this phase, a slowdown in rates of technological growth of civilization begins. Urban population growth falls to 260 people per year, and growth of the index of urbanization decreases to 0.0002 per cent per year.

Phase 4 (years 510–680 of the simulation). Accelerating expansion of the tribal periphery.

At this phase the positive feedback mechanism accelerating the counterattack of the tribal periphery works at full capacity. The territory controlled by the civilizational center is reduced by 2.5 million km² and the population of the civilizational center is reduced from 24.1 to 21.7 million people. This reduction is only partially compensated by the increase in population of the tribal periphery and hinterland of the World System; as a result, the total population growth rate of the World System falls from 0.043 to 0.01 per cent per year. The rates of technological growth of civilization are reduced from 0.076 to 0.068 per cent per year. Starting from the year 614 of our computer simulation, the continuing growth of urban population in the territory unoccupied by ‘barbarians’ ceases compensating for the reduction in urban population as a result of counterattack of tribal periphery, and the total urban population begins to decrease. The World System urbanization index begins to decrease even earlier, starting from the year 577 of the simulation.

Phase 5 (years 680–935 of the simulation). Slowdown of the expansion of the tribal periphery.

During this phase a system of feedbacks reducing the vigor of counterattack of tribal periphery comes to the foreground (Fig. 7).

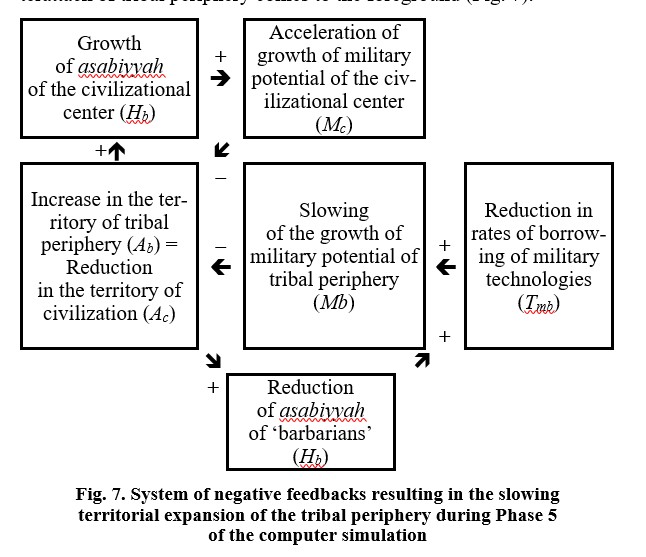
Despite its slowdown, the continuing counterattack of the tribal periphery throughout this phase leads to substantial consequences. The area of the territory controlled by the civilizational center is reduced almost twofold. The population of the civilizational center falls from 21.73 to 15.97 million people. Until the year 730 of the simulation, this reduction is compensated to a lesser degree than earlier by the increase of population of tribal periphery and hinterland of the World System; therefore, the growth rate of the World System total population reduces almost to zero. Later, the effect of the slowdown of expansion of tribal periphery begins to manifest; against the background of continuing acceleration of growth rates of population of the tribal periphery and hinterland, it leads to a renewal of the increase in growth rates of the total population of the World System. This growth is initially very slow, for example, growing by only 0.002 per cent between years 730 and 789 of our simulation, and even in the year 935, the population growth rate of the World System remains extremely low, 0.027 per cent per year. In contrast, at the beginning of the first phase it was 0.37 per cent per year – ten times higher. The technological growth rates of civilization continue to decrease (from 0.068 to 0.05 per cent per year). The urban population declines from 403,000 to 344,000 people (at the same time the effect of the decline of the vigor of the tribal counterattack begins to manifest itself – the absolute rates of decrease in urban population reach a maximum in years 817–838, and then begin to decline). The World System urbanization index falls from 0.0116 to 0.0095 (though the rate at which this indicator declines is reduced starting from the year 865 of our simulation).

Phase 6 (years 935–2885 of the simulation). Expansion of the tribal periphery reaches its peak. Approximate balance of forces. Civilization launches a counterattack.

During this phase, the territory of tribal periphery as compared to the territory of the civilizational core changes rather slowly, at a rate of no more than 0.01 million km² per year (reaching an inflection point of just 0.5 km² per year in year 2047 of our simulation). At the first stage of this phase (years 935–2047), the action of the negative feedback described in Fig. 7 produces its logical conclusion: the military potentials of civilization and tribal periphery become equal, and the expansion rates of the tribal periphery decline to zero. However, the rates of technological development (including the growth rates of military technologies) of civilization continue to outpace those for tribal periphery. As a result, the military potential of civilization begins to exceed that of the tribal periphery, and civilization begins its counterattack (starting from the civilization territory of just 1.23 million km²) in year 2048 of our simulation. At first it proceeds very slowly (only 1.5 km² during the first year of the ‘counterattack’); but the beginning of civilization's counterattack leads to the formation of a system of positive feedbacks (described in Fig. 4), giving more and more noticeable results every year – growth of the territory of civilization leads to an increase in its population, which leads to the growth of military potential both directly and through acceleration of technological growth rates; the growth of its military potential leads to a further increase in its population, which leads to further acceleration of growth of its territory, etc. As a result, the territory of civilization grows from 1.23 million km² in year 2048 to 2.94 million km² by the end of this phase at an increasing (but still generally rather slow) rate.

The growth rates of the total population of the World System continue to increase throughout all the sixth Phase, but slowly, at a rate rising from 0.027 to 0.12 per cent per year, remaining lower than the rates characteristic of the beginning of Phase 1. The population of the civilizational center continues to fall until year 1438 of our simulation, declining from 15.97 to 12.73 million. Its growth then resumes, and, by the end of the phase, the civilization population reaches 38.5 million, considerably exceeding the level reached in Phases 1–3. The reduction of technological growth rate of civilization continues till year 1439 of the simulation (declining from 0.05 to 0.04 per cent a year), and then this rate begins to grow rapidly, reaching 0.12 per cent per year by 2885 (considerably exceeding the level reached in Phases 1–3). The World System urban population continues to decline till year 1169 of the simulation (decreasing from 344,000 to 320,000 people) then its growth resumes, gradually accelerating, until by the end of Phase 6, the urban population of the World System reaches 2,340,000. The World System urbanization index continues to fall much longer – until year 1600 of our simulation, declining from 0.0095 to 0.0074 – and then begins to grow with gradual acceleration, reaching 0.0206 by the end of Phase 6. Note that phases 3–6 of the interaction between the World System civilization center and its tribal periphery are rather well described in Chapter 3 of War! what is it Good For? (Morris 2014: 112–164).

Phase 7 (years 2885–3209 of the simulation). As a result of a vigorous counterattack civilization completely subordinates Zone 2, absorbing the whole tribal periphery.

During this phase, there is a rapid growth of all the modeled indicators of the level of development of the World System. By year 3065 of the computer simulation, the urban population of the World System reaches the level of 10 million, and the World System urbanization index exceeds 10 per cent in 3123. In reality at this level, civilization would already have to contact with the extensive hinterland of the World System (which managed to achieve rather high levels of population and technological development during our simulation), whereas the World System hinterland would transform into the new tribal periphery of civilization. With certain values of parameters, this transformation could lead to a new counterattack of the tribal periphery at a higher level. However, incorporating these parameters would lead to additional complication of the model from which we have decided
to refrain at this stage.⁴

It is remarkable that the correlation between technological development and urbanization of the World System generated by this model is surprisingly similar to what we have seen (see Korotayev and Grinin 2021: Fig. 4) for the empirical estimates of the level of technological development of the World System and its level of urbanization (Figs. 8–10).

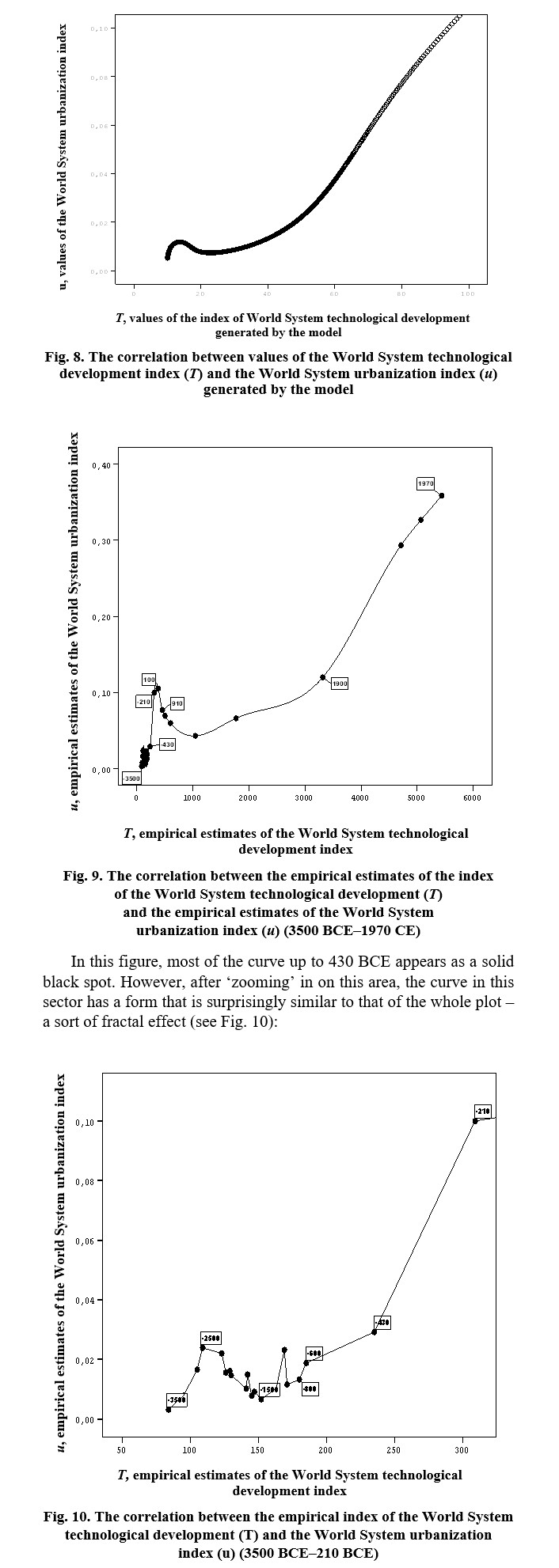
The shapes of all three curves are amazingly similar: in the initial part of the figure, even rather small technological growth is followed by very noticeable growth of urbanization of the World System. This is followed by a pronounced interval in which further technological growth is accompanied by a decrease of urbanization level, which is changed by an interval where technological growth is accompanied by slow growth of urbanization which is followed by a stretch where technological growth is accompanied by rapid growth of urbanization with a subsequent new interval of relative slowdown.

It is worth noting that formal indicators of correlation for model values of these two variables (R = 0.95, R² = 0.903) are almost identical to the ones we calculated for empirical values of these variables (see note to Fig. 4 in Korotayev and Grinin 2021).

Perhaps, this is not purely coincidence, since this correlation – both in our model and in reality – was generated by mechanisms similar in many respects. Thus, the impact of the tribal periphery on the central (‘civilized’) territories of the World System in the first millennium CE led to noticeable barbarization and de-urbanization of many of these zones, as a result of which the World System urbanization index considerably decreased. At the same time, the rates of technological growth (both in our model and in reality) decreased, but tech-nological growth did not stop completely: new inventions and discoveries continued to be made (especially in those zones of the World System which underwent the least de-urbanization). As a result, the decrease in the level of urbanization at that time was followed by some (albeit decelerated) growth of its level of technological development, which caused an apparent negative correlation reducing the level of the general positive correlation between the variables in question.

Note that in our computer simulation the final phases of conquest of barbarian periphery by civilization are not free of drama. Not long before the end of the full conquest of the barbarian periphery by civilization, its asabiyyah falls to zero (‘dizziness with success’?) which leads to a fast and powerful counterattack of the tribal periphery, burst of civilization's asabiyyah, and an even more rapid final submission of the tribal periphery (Fig. 11).

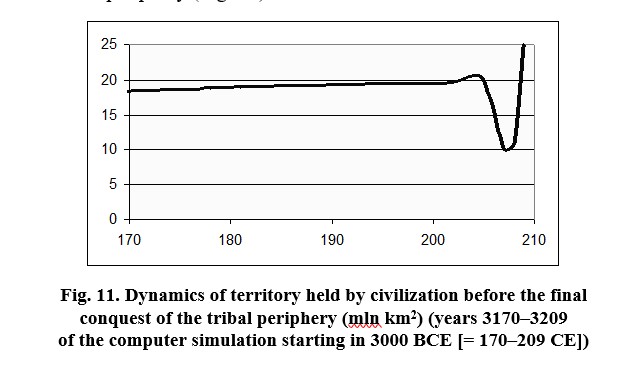
In our opinion, quite a probable scenario of events is modeled here; fortunately, however, it does not appear to have ever been realized in real history of the World System (though the events of 9/11, perhaps, are analogous to some slight degree).

* * *

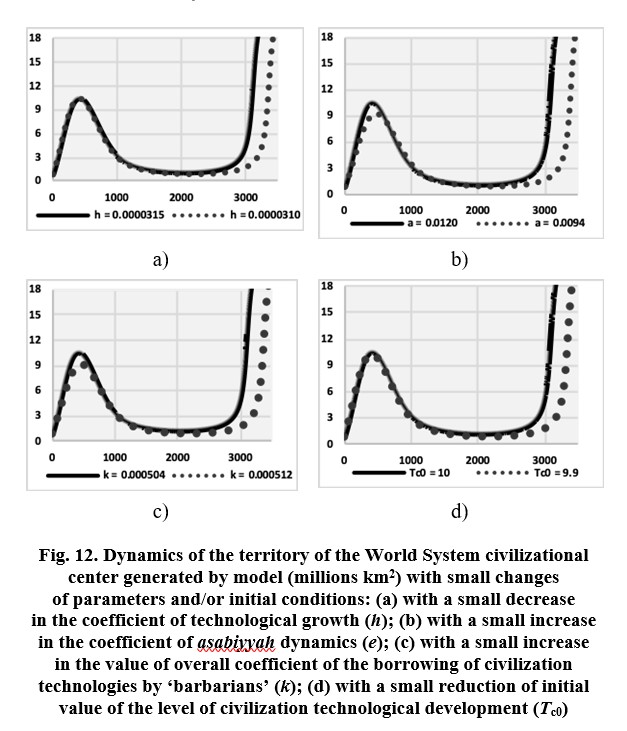
The numerical study of influence of parameter values on the dynamics of our model shows that the key parameters determining the duration of phases are as follows: the coefficient of innovative activity (h in Eq.⁵ (8)) defining the rates of technological growth; the coefficient of territorial expansion (a in Eq. (1)); the coefficient of borrowing of technologies from civilization by ‘barbarians’ (k in Eq.(17)), particularly military technologies (n in Eq.(19)); the coefficient of dynamics of asabiyyah (e in Eqs. (4) and (5)), and the relationship between the coefficient of military participation of ‘barbarians’ (b) and civilization (c).

A small reduction of the value of coefficient h with respect to the value mentioned in the note to Figs. 1–3 leads to some reduction of the duration of Phases 1–3, and a significant increase in the duration of other phases, but most notably of Phase 6 (‘relative equilibrium of forces’). With a reduction in the coefficient of technological development (h) the rates of historical development slow down (see Fig. 12a).

Similar results are produced by several changes: a small reduction of the coefficient of territorial expansion (a, Fig. S1 in the Supporting Online Materials), or small increase in the values of the coefficient of asabiyyah dynamics (e, Fig. 12b), coefficient of borrowing of technologies from civilization by ‘barbarians’ (k, Fig. 12c), particularly military technologies (n, Fig. S2), and a small increase in the gap between the coefficients of military participation of population of the tribal periphery and civilizational core (b/c, Fig. S3), small reduction of initial values of the level of technological development of civilization (T_c0, Fig. 12d), its territories and asabiyyah, and a small increase in the initial values of the level of technological development, territory, and asabiyyah of the tribal periphery.

The small changes of parameters and initial conditions of the model described above lead to a reduction in the territory civilization controls during the first wave of its expansion (Phases 1–2.5), and an increase in the duration and intensity of the counterattack of the tribal periphery (Phases 2.5–5.5). As a result, the zone remaining under the control of civilization at the maximum of the tribal counter-expansion is reduced. Further changes of parameters and initial conditions in this direction leads to significant changes of the overall picture of dynamics and implementation of a significantly different scenario. If (as a result of the tribal expansion) the civilization zone is reduced below 1 million km², it means that in that model simulation the tribal periphery conquers part of the central civilization zone (Zone 1) with an especially high natural productivity. In the model simulation, this leads to a pronounced strengthening of ‘barbarians’ (even as their counterattack approaches its exhaustion) and a serious weakening of civilization. In our simulations, civilization could launch a counterattack only if the ‘barbarians’ managed to take no more than 1–2 per cent of Zone 1. Otherwise, rapid, pronounced strengthening of ‘barbarians’ accompanied by rapid, pronounced weakening of civilization leads to a new acceleration of tribal expansion and a quick final conquest of civilization by ‘barbarians’. Thus, a new phase is added – Phase 6’, the phase of the new acceleration of tribal expansion and final conquest of the civilization by ‘barbarians’ – and Phases 6.5–7 disappear.

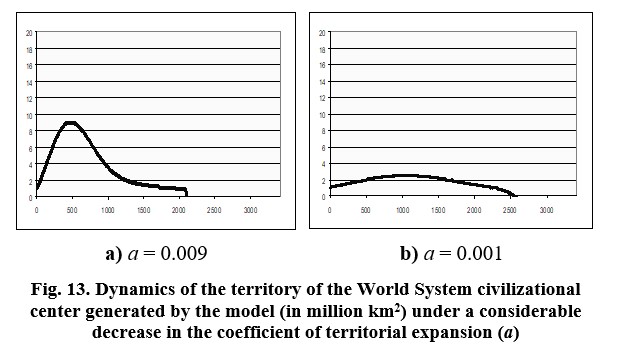
Further reduction of the coefficient of territorial expansion (a) reduces the size of the territory under the control of civilization at the peak of its territorial expansion, but at the same time postpones ‘barbarian occupation’, prolonging the life of civilization (Fig. 13).

On the other hand, further reduction of the coefficient of innovative activity (h) or increase in the values of the coefficient of asabiyyah dynamics (e), the coefficient of borrowing technologies of civilization by ‘barbarians’ (k) (and, in particular, military technologies (n)), as well as further increases in the gap between coefficients of military participation of population of the tribal periphery and civilizational core (b/c), further reduction of the initial values of the level of technological development of civilization (T_c0, Fig. S4), its territory and asabiyyah, and also further increase in initial values of the level of technological development, territory, and asabiyyah of the tribal periphery lead to reduction of the ‘life of civilization’, to its more rapid conquest by ‘barbarians’ (see Figs. S4–S9 in the Supporting Online Materials, see https://www.sociostudies.org/journal/files/seh/2021_2/supporting_materials.php).

With such parameter values the model describes quite a realistic scenario. Indeed, with a certain set of parameters the expansion of civilization could create such a powerful tribal periphery that its counterattack could destroy the civilization. The classic example here is the conquest of Rome by ‘barbarians’; Rome's expansion in many respects gave ‘barbarians’ the very strength which eventually helped them to break down their formidable opponent (see, e.g., Turchin 2005).

Beyond a certain limit we develop a scenario of more and more rapid conquest of civilization by ‘barbarians’ without a phase of initial civilizational expansion (Fig. 14).⁶

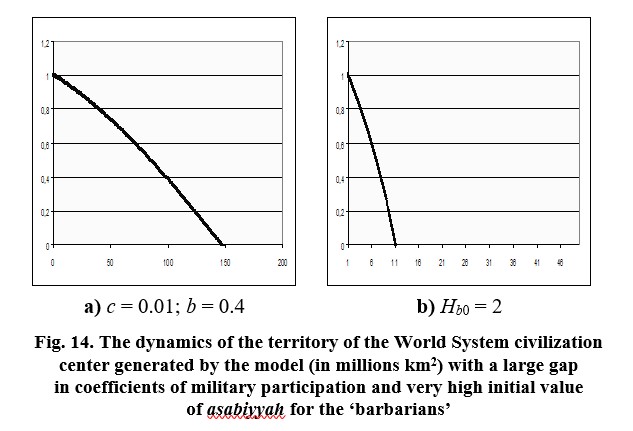
In this case we have a rather banal scenario of the final conquest of civilization by ‘barbarians’ whose military superiority has been predetermined by initial parameters and initial conditions, while civilization (with the same parameters and initial conditions) has no chance to effectively resist tribal expansion.⁷

In case of a small change of parameters and initial conditions in the opposite direction in relation to the parameters and initial conditions described in the note to Figs. 1–3,⁸ we see in our computer simulations some increase in the duration of phases of the initial expansion of civilization, the territory occupied by it during expansion (as well as the territory retained by it at the peak of ‘barbarian’ counterattack), and a reduction in the duration of all subsequent phases, in particular, Phase 6 (‘relative balance of forces’) (Figs S10–S16 in the Supporting Online Materials,  https://www.sociostudies.org/journal/files/seh/2021_2/supporting_materials.php).

With further changes of parameters in this direction (and, in particular, with combined changes of several), one can observe a further increase in duration of phases of the initial expansion of civilization, the area of the territory occupied by it during the first expansion phases (as well as the territory kept by it at the peak of ‘barbarian’ counterattack), and again, a reduction of the duration of all subsequent phases, in particular Phase 6 (‘relative balance of forces’). Gradually, the duration of Phases 3–6 is reduced to zero and they disappear, whereas Phases 1–2 eventually merge with Phase 7. As a result, we have only Phase 1, and further change of parameters in this direction leads only to reduction of the period required for civilization to conquer its tribal periphery (see Figs. S17–S20 in the Supporting Online Materials, see at   https://www.sociostudies.org/journal/files/seh/2021_2/supporting_mate-rials.php).

Let us note that in all cases we deal with quite realistic scenarios of interaction between civilizational center and tribal periphery. Historically, the contact between a technologically advanced (and rapidly developing) civilization with an extremely technologically underdeveloped periphery incapable of rather quickly borrowing the technologies of civilization, has led to the accelerated conquest of the periphery by civilization (the British colonization of Australia presents a rather salient example of such a scenario, whereas, e.g. in North America in the seventeenth – nineteenth centuries one can find cases of Scenarios 2 and 3 [see Table 1 below]).

Thus, depending on the parameters and initial conditions, the model we offer can mathematically describe seven significantly different scenarios of interaction between civilizational center and tribal periphery (Table 1).

Thus, the scenario displayed in Figs. 1–3, and most precisely describing the influence of interaction between the civilization center and tribal periphery on World System development, is intermediate among the scenarios described in Table 1. One can suppose that this is not a coincidence; in fact, there are some grounds to maintain that this interaction could have the historically attested impact only with intermediate parameter values. ‘Barbarians’ could not effectively confront the expansion of civilization and launch a massive counterattack with very low values of coefficients e, k, n and b – that is, if their collective solidarity were not sufficiently amplified under the influence of pressure from civilization; if they failed to adopt vitally important technologies of civilization (including military ones) quickly enough; or if they did not possess a much higher military participation ratio. On the other hand, a too high value of these parameters would have made the expansion of civilization of the World System impossible, or would even have led (at especially high values of these parameters) to a rapid conquest of civilization by ‘barbarians’ before the expansion of civilization could start. One can say the same of the values of all other significant parameters of the model, and of the values of the initial conditions. For example, if at the time of clash of civilization with the tribal periphery, the relative level of its technological development had been too low, it would not have been able to begin expansion at all, and with an extremely high value it would have rapidly subordinated the periphery that would be incapable of offering any effective resistance.

On the other hand, we can easily notice that practically all the scenarios described above were observed in the history of the World System at the level of particular civilization zones and their peripheries. In many respects, this is precisely why the total dynamics of the World System appears to be the closest to the intermediate scenario of the model. Of course, in our case the fit of theoretical curve with empirical estimates is still far from ideal – which is not surprising, since nobody would claim that the interaction between civilization core of the World System and its tribal periphery was the only factor that defined the characteristic form of the curve of world urbanization dynamics.

What is really surprising for us, is the fact that the suggested model after all appeared capable to describe the general form of this dynamics so precisely (though, of course, imperfectly). Hence, this suggests that the interaction between the civilization core of the World System and its barbarian periphery was really an important factor making a notable contribution (until very recently) to giving the peculiar form to the curve of the world urbanization dynamics.

The proposed model suggests that, in the history of the World System development, the important component of World System phase transitions А₁ and А₂ could be not only the movement of its core to a new level of complexity, but also the formation of barbarian periphery of an essentially new type capable to offer much more effective resistance to civilization expansion and to mount successful counterattacks that, apparently, could make a noticeable contribution to the formation of the ‘attractor effect’ during periods В₁ and В₂.

There are some other points that also seem to explain why this model, which takes into account only one factor of World System dynamics (and not always the most important one), was able to generate a curve that so well describes empirically observed historical macrodynamics. It is likely that this model describes the general developmental logic of the World System, within which the hyperbolic growth of its civilizational core creates powerful forces restricting growth at certain phases of its development – or, to be more exact, moving the World System to a new, lower, hyperbolic trajectory (see, e.g. Korotayev 2006c, 2007a, 2007b, 2008, 2009, 2013, 2018, 2020; Korotayev, Mal-kov, Khaltourina 2007; Grinin, Korotayev 2009b; Korotayev, Malkov 2016).

We earlier described one such factor (which probably affected the World System dynamics in Phase В₂ to an extent not less, though probably not greater than the effect of the interaction between civilization center and tribal periphery) as follows:

The growth of the World System population by the end of the first millennium BCE up to 9-digit numbers produced a breeding ground that led to an almost inevitable appearance of a new generation of more lethal and epidemically destructive pathogens that could not reproduce themselves in smaller populations (Diamond 1999: 202–205; McNeill 1993; Korotayev, Malkov, Khaltourina 2005: 105–113; 2006a), whereas the level of health care technologies achieved by the World System by the beginning of the first millennium CE turned out to be totally inadequate for the radically increased level of pathogen threat. Thus, the Antonine and Justinian's pandemics led to global depopulations of the second and sixth centuries, contributing in a very significant way to the slowdown of the World System demographic growth in the first millennium CE. Note that due to this, since the early first millennium CE the role of health care technologies as a determinant of the carrying capacity of the Earth dramatically increases, which at least partly accounts for the change of the hyperbolic growth regime (Korotayev, Malkov, Khaltourina 2006b: 159; 2007: 206).

It is vital that the logic of action of this factor is extremely similar to the logic of action of the factor analyzed in this article. In the both cases, the hyperbolic growth of civilization creates powerful forces that block growth. On the other hand, the pressure of the tribal periphery was able to stimulate the growth of military potential of civilization, whereas pathogenic attacks on the World System eventually stimulated development of health care technologies, which allowed the World System to repulse these attacks more successfully and renew its hyperbolic growth.⁹

The logic of this factor is similar to the logic of another factor that apparently had an even greater influence on the World System dynamics in phase В₁, than the effect of interaction between the civilizational center and tribal periphery – the factor of environmental degradation under the influence of the hyperbolic growth of civilization. This factor is most evident in the history of ancient Mesopotamia, whose curve of urbanization dynamics in the forth – early second millennia BCE defined the general shape of the World System urbanization dynamics curve to a very considerable extent. As is well known, the explosive growth of civilization in this region led to catastrophic soil salination in its most developed zone – in Lower Mesopotamia – which, in turn, led to a decrease in rates of demographic and urbanization growth, resulting in negative values in the middle of the third millennium. On the other hand, environmental degradation stimulated the technological growth in the region, which led in the first millennium CE to the restoration of carrying capacity values to the levels present at the beginning of the third millennium BCE, and then to its noticeable expansion (Dyakonov 1983: 272, 330; Chubarov 1991; Roberts 1998: 175).

These facts explain to some extent a paradox that can be noticed above, in Figs. 1–3, and 8–10 (as well as in in Figs. 1–2 in Korotayev and Grinin 2021; see also Korotayev 2006b). The point is that for the interaction between civilization center and tribal periphery to produce an effect similar to that actually observed, the territory under the control of civilization should be decreased manifold and remain at an extremely low level for a very long period, which apparently did not happen in reality. Apparently, what was not ‘consumed’ by ‘barbarians’ at ‘sinks’ in Figures 1–2 corresponding to phases В₁ and В₂ was mostly ‘eaten away’ by pathogenic attacks and environmental degradation.

Finally, let us dwell upon some other factors that seem to be relevant for modeling of the long-term dynamics of the World System. We described one of these factors earlier in the following way:

Some hint here seems to be suggested by mathematical models (0.11)–(0.13)–(0.12) and (0.13)–(0.14)¹⁰ described in the Introduction. According to these models, any long-term decrease of per capita surplus (S) must lead to the decrease of population growth rates and, hence, the slow-down of technological growth. In the meantime, by the end of the Axial Age we seem to observe a World System trend towards the decline of precisely this indicator. This was connected not with decline of production, but rather with the growth of m, the per capita product that is necessary for population reproduction with zero growth rate, the ‘minimum necessary product’ (MNP). In the first millennium BCE the rapid population growth sustained the hyperbolic growth of the complexity of sociopolitical infrastructures (on the other hand, of course, the hyperbolic population growth was also sustained by a hyperbolic growth of sociopolitical complexity – once more we are dealing here with the positive feedback phenomenon). However, the radical increase in sociopolitical complexity meant a radical increase in the MNP, as the substantial expenses necessary for the normal functioning of these sociopolitical infrastructures should be regarded, in this context, as a part of the minimum necessary product (rather than as surplus). Indeed, by the end of the first millennium BCE the World System population reached 9-digit numbers; even a simple reproduction (at zero growth rate) of so huge a population required maintenance of normal functioning of all those infrastructures (transportation, judicial, administrative and other such subsystems). Within such a context, if the product produced this year by a peasant is only sufficient to secure the survival of himself and his household, but not sufficient to pay any taxes, it is impossible to say that this peasant has produced this year the minimum necessary product. In fact, what he has produced this year is smaller than the MNP. Indeed, as the experience of post-Axial centuries showed on numerous occasions, in supercomplex agrarian societies the decrease of per capita production (usually as a result of relative overpopulation) down to a level that did not allow the population to pay taxes led to the disintegration of sociopolitical infrastructures and political-demographic collapse (see Korotayev, Malkov, and Khaltourina 2006b: Chapters 1–4). ¹¹ There are grounds to maintain that the rapid growth of the MNP in the 1st millennium BCE exceeded the growth of the equilibrium per capita production, which resulted in the long-term decrease of real S, and, hence, the decrease of the World System population growth rates. On the other hand, it led to the decrease of sociopolitical system stability, and, hence, to the increase in the importance of the role of cyclical and chaotic components of the macrohistorical dynamics in comparison with the trend component (Ibid.: 159–160; 2007: 206–207).

Obviously, in this case we also deal with a force that was created by the World System's hyperbolic growth and that blocked for some time the further hyperbolic growth of the World System.

CONCLUSION

In this article we have offered an analysis of a mathematical model of the influence of one of the major factors of the World System macrodynamics throughout most of its history (since the ‘urban revolution’) – the factor of interaction between civilizations and their tribal peripheries. The proposed mathematical model has turned out to be capable to describe the influence of interaction between civilizational core of the World System and its tribal periphery on the formation of the specific curve of the world urbanization dynamics. It describes rather adequately completion of the phase transition, behavior of the system in the attraction basin and beginning of the phase transition to the attraction basin of the new attractor. This models helps to identify the role of the factor of interaction between the civilizational core and tribal periphery in the formation of attractor effect during the completion of phase transition, that is, it helps to understand the reason why there was observed not only slowdown of growth rates of the main indicators of the World System development after completion of phase transitions during its development, but also their falling with the subsequent temporary stabilization near some equilibrium level.

Of course, in our case the fit of theoretical curve with empirical estimates is still far from being ideal – which is not surprising, since nobody would claim that the interaction between civilization core of the World System and its tribal periphery was the only factor that defined the characteristic form of the curve of world urbanization dynamics.

What is really surprising for us is the fact that the model offered actually appeared capable of describing the general form of these dynamics so precisely (though, of course, imperfectly). This suggests that the interaction between the civilization core of the World System and its tribal periphery was really an important factor making a notable contribution (until very recently) to giving rise to the peculiar form of the curve of the world urbanization dynamics.

The proposed model suggests that, in the history of World System development, the important component of World System phase transitions А₁ and А₂ may be not only the movement of its core to a new level of complexity, but also the formation of a tribal periphery of an essentially new type, capable of offering much more effective resistance to civilization’s expansion, and of mounting successful counterattacks that, apparently, could make a noticeable contribution to the formation of the ‘attractor effect’ during periods В₁ and В₂.

Finally, we again highlight a point that seems to explain why our model, which takes into account only one factor of World System dynamics is able to generate a curve that so well describes empirically observed historical macrodynamics. This model most likely describes the general development logic of the World System within which the hyperbolic growth of its civilizational core creates powerful forces restricting its growth at certain phases of development – to be more exact, one that moves the World System to a new, lower, hyperbolic trajectory.

Regarding the possible ways of the further development of the proposed model, it appears interesting to study how the model would react in different regions. For example, above we discussed the impact of pathogens on the World System, but in most cases the impact will be unevenly distributed. It would be interesting to study if the regions left relatively unscathed would get a ‘boost’ in expansive capability, whether that would depend on their situation along the civilization/barbarian frontier and so on.¹²

ACKNOWLEDGEMENTS

This research was performed according to the Development program of the Interdisciplinary Scientific and Educational School of Lomonosov Moscow State University ‘Mathematical methods of analysis of complex systems’.

FUNDING

This research has been supported by the Russian Science Foundation (Project No 20-61-46004).

NOTES

1 Largely as a result of increasing diffusion of high technologies of civilization in the territories of Zone 2 subordinated by it, the growth of the carrying capacity there, and, therefore, the population.

2 In connection both with accelerating technological growth of civilization and with the growth of the share of ‘civilized’ population in the total World System population.

3 In connection both with the growing urbanization in civilizational zone, and with the accelerated growth of its population as a result of territorial expansion.

4 This model also does not describe the withdrawal of the World System from the blow-up regime. In theory, in our case it might be possible, having described basic population dynamics by means of the following equations: dN/dt =
= r∙dT/dt ∙ (1–l); dN/dt £ 0,04; dl/dt = s∙dT/dt ∙ (1–l) (where l is a share of literate population, and r and s are constants), and basic urbanization dynamics by means of the following equations: du/dt = v∙dT/dt × (u_lim – u) (where u_lim is a maximum possible share of urban population, and v is a constant). For justification of equations of this type, see Korotayev 2006c; Korotayev, Malkov, and Khaltourina 2006a, 2006b, 2007; Korotayev, Komarova, and Khaltourina 2007. However, we decided not to incorporate them in this case to avoid excessive complication of the model, especially since our computer simulation does not include the description of withdrawal of the World System from the blow-up regime, and we have previously offered mathematical models with such a description (see e.g. Korotayev 2006c; Korotayev, Malkov, Khaltourina 2006a, 2006b, 2007; Korotayev, Komarova, Khaltourina 2007).

5 See Korotayev and Grinin 2021 for a description of the equations.

6 We should also note that the change of parameters of the model in this direction is meaningful only to a certain degree. Say, the coefficient of military participation of ‘barbarians’ (b), by definition cannot exceed 1.0; even a value of 1.0 describes an unrealistic scenario because the entire population of any society (including, as we know, newborn babies and very old men and women) cannot actually take part in combat. Similar restrictions also exist for all other parameters and initial conditions of the model.

7 At the same time, if, say, the conquest of civilization by ‘barbarians’ within the model is brought about by assigning a higher initial value of asabiyyah (H) to the ‘barbarians’, the scenario can be interpreted within Ibn Khaldun's tradition (see, e.g., Ibn Khaldun 1958, 2004; Alekseev and Khaltourina 2004; Turchin 2003, 2007; Korotayev, Khaltourina 2006; Korotayev 2006a, 2007c, 2007d; Inan 1933; Mahdi 1937) as the conquest of a low-asabiyyah civilization by high-asabiyyah ‘barbarians’, which does not ‘end history’, but begins a new historical round, a new ‘Khaldunian’ dynastic cycle – but this would result in a quite different model.

8 With a small increase of the coefficient of technological growth (h) and the coefficient of territorial expansion (a), or with a small reduction of the values of the coefficient of asabiyyah dynamics (e), the coefficient of borrowing of civilization technologies by ‘barbarians’ (k) and, in particular, military technologies (n); with a small decrease of the gap between military participation ratios of the tribal periphery and civilizational core (b/c); with a small increase in the initial values of the level of technological development of civilization (T_c0), its territory and asabiyyah; and with a small reduction of the initial values of the level of technological development, territory and asabiyyah of the tribal periphery.

9 It appears appropriate to recollect at this point that this growth continued up to the early 1970s, when the World-System started to withdraw from the hyperbolic growth regime (i.e. the blow-up regime) due to the force created by its hyperbolic growth, but these were forces of another kind (Korotayev, Malkov, Khaltourina 2006a, 2006b, 2007).

10 These numbers refer to equations presented in the Introduction to Korotayev, Malkov, and Khaltourina 2006b.

11 See also, e.g., Nefedov 2001, 2002a, 2002b, 2003, 2004, 2005, 2007, 2013; Turchin 2003: 121–127; Turchin and Nefedov 2009.

12 See Part 3 of the supporting online materials for a discussion of other possible routes for further development of the model.

13 مقدمة ابن خلدون / تأليف عبد الرحمن ابن خلدون. القاهرة: دار الفجر في التراث، 2004.

14 القاهرة: دار الكتب المصرية، 1933. ابن خلدون : حياته و تراثه الفكري / تأليف محمد عبد الله عنان.

REFERENCES

Alekseev, I., Khaltourina, D. 2004. Ibn Khaldun and the Theory of Demographic Cycles in Modern Social Sciences. In Steblin-Kamensky, I. M. et al (eds.), School of the Young Orientalist – 2004 (pp. 129–133). St. Petersburg: St. Petersburg State University. Original in Russian (Алексеев И. Л., Халтурина Д. А. Ибн Халдун и теория демографических циклов в современных социальных науках. Школа молодого востоковеда – 2004 / Ред. И. М. Стеблин-Каменский, и др., с. 129–133. Санкт Петербург: СПбГУ).

Chubarov, V. 1991. The Middle Eastern Locomotive: The Developmental Pace of Technique and Technology in the Ancient World. In Korotayev, A., and Chubarov, V. (eds.), Archaic Society: Main Problems of Sociology of Development. Vol. 1 (pp. 92–135). Moscow: History Institute. Original in Russian (Чубаров В. В. Ближневосточный локомотив: темпы развития техники и технологии в древнем мире. Архаическое общество: узловые проблемы социологии развития / Ред. А. В. Коротаев, В. В. Чу-баров, т. 1, с. 92–135. М.: Институт истории СССР АН СССР).

Diamond, J. 1999. Guns, Germs, and Steel: The Fates of Human Societies. New York: Norton.

Dyakonov, I. (Ed.) 1983. History of the Ancient East. Vol. I. Mesopotamia. Moscow: Nauka. Original in Russian. (Дьяконов И. (Ред.) История Древнего Востока. Том 1. Месопотамия. Москва: Наука). 

Grinin, L., Korotayev, A. 2009b. Social Macroevolution: Growth of the World System Integrity and a System of Phase Transitions. World Futures 65 (7): 477–506.

Ibn Khaldūn, `Abd al-Rahman. 1958. The Muqaddimah: An Introduction to History. New York: Pantheon Books (Bollingen Series, 43).

Ibn Khaldūn, `Abd al-Rahmān. 2004. Muqaddimat ibn Khaldūn. al-Qāhirah: Dar al-Fajr li-l-Turāth.¹³

‘Inān, Muḥammad ‘Abd Allāh. 1933. Ibn Khaldūn: ḥayātu-hu wa-turāthu-hu al-fikriyy. al-Qāhirah: Dār al-Kutub al-Misriyyah.¹⁴

Korotayev, A. 2006a. Long-Term Political-Demographic Dynamics of Egypt: Cycles and Trends. Moscow: Vostochnaya literatura. Original in Russian (Коротаев А. В. Долгосрочная политико-демографическая динамика Египта: циклы и тенденции. М.: Вост. лит-ра).

Korotayev, A. 2006b. The World System Urbanization Dynamics: A Quantitative Analysis. In Turchin, P., Grinin, L., Korotayev, A., and de Munck, V. C. (eds.), History & Mathematics: Historical Dynamics and Development of Complex Societies (pp. 44–62). Moscow: KomKniga/URSS.

Korotayev, A. 2006c. The World System History Periodization and Mathematical Models of Socio-Historical Processes. In Grinin, L., de Munck, V. C., and Korotayev, A. (eds.), History & Mathematics: Analyzing and Modeling Global Development (pp. 39–98). Moscow: KomKniga/URSS.

Korotayev, A. 2007a. Compact Mathematical Models of World System Development, and How They can Help us to Clarify our Understanding of Globalization Processes. In Modelski, G., Devezas, T., and Thompson, W. R. (eds.), Globalization as Evolutionary Process: Modeling Global Change (pp. 133–160). London: Routledge.

Korotayev, A. 2007b. Macrodynamics of the World System Urbanization: A Quantitative Analysis. In Malkov, S., Grinin, L., and Korotayev, A. (eds.), History and Mathematics: Macrohistorical Dynamics of the Society and State (pp. 21–39). Moscow: Komkniga/URSS. Original in Russian (Коротаев А. В. Макродинамика урбанизации Мир-Системы: количественный анализ. История и Математика: Макроисторическая динамика общества и государства / Ред. С. Ю. Малков, Л. Е. Гринин, А. В. Коротаев, с. 21–39. М.: КомКнига/URSS).

Korotayev, A. 2007c. Sociological Theory of Abd al-Rahman ibn Khaldun (1332–1406) as a Methodological Basis for the Mathematical Modeling of Political-Demographic Dynamics of Medieval Еgypt. In Dilek, Z. (ed.), 38. ICANAS. Abstracts (p. 310). Ankara: ICANAS.

Korotayev, A. 2007d. Sociological Theory of Abd al-Rahman ibn Khaldun as a Methodological Basis for the Mathematical Modeling of Long-Term Political-Demographic Dynamics. In Malinetsky, G. G. (ed.), Abstracts of 2^nd International conference Mathematical Modeling of Historical Processes Preprint, Inst. Appl. Math., the Russian Academy of Science (pp. 31–34). Moscow: Institut Prikladnoy matematiki. Original in Russian (Коротаев А. В. Социологическая теория Абд Ар-Рахмана ибн Халдуна как методологическая основа математического моделирования долгосрочной политико-демографической динамики. Тезисы докладов II Международной конференции Математическое моделирование исторических процессов / под ред. Г. Г. Малинецкого. М.: ИПМ им. М. В. Келдыша РАН).

Korotayev, A., Grinin, L., and Grinin, A. 2021. A Mathematical Model of Interaction between Civilization Center and Tribal Periphery: A description. Social Evolution & History 20 (2): 50–78.

Korotayev, A., and Khaltourina, D. 2006. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends in Africa. Moscow: KomKniga/URSS.

Korotayev, A., Komarova, N., and Khaltourina, D. 2007. Laws of History. Secular Cycles and Millennial Trends. Demography. Economy. Wars. Moscow: Komkniga/URSS. Original in Russian (Коротаев А. В., Комарова Н. Л., Халтурина Д. А. Законы истории. Вековые циклы и тысячелетние тренды. Демография. Экономика. Войны. М.: КомКнига/ URSS).

Korotayev, A., and Malkov, A. 2016. A Compact Mathematical Model of the World System Economic and Demographic Growth, 1 CE – 1973 CE. International Journal of Mathematical Models and Methods in Applied Sciences 10: 200–209.

Korotayev, A., Malkov, A., and Khaltourina, D. 2005. Laws of History: Mathematical Modeling of Historical Macroprocesses. Demography, Economy, Wars. Moscow: URSS. Original in Russian (Коротаев А. В., Малков А. С., Халтурина Д. А. Законы истории: Математическое моделирование исторических макропроцессов. Демография, экономика, войны. М.: КомКнига/URSS).

Korotayev, A., Malkov, A., and Khaltourina, D. 2006a. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: KomKniga/URSS.

Korotayev, A., Malkov, A., and Khaltourina, D. 2006b. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends. Moscow: Kom Kniga/URSS.

Korotayev, A., Malkov, A. S., and Khaltourina, D. A. 2007. Laws of History. Mathematical Modeling of Development of the World System. Demography. Economy. Culture. Moscow: Komkniga/URSS. Original in Russian (Коротаев А. В., Малков А. С., Халтурина Д. А. Законы истории: Математическое моделирование развития Мир-Системы. Демогра-фия, экономика, культура. М.: КомКнига/URSS).

Mahdi, M. 1937. Ibn Khaldūn's Philosophy of History. A Study in the Philosophical Foundation of the Science of Culture. London: Allen & Unwin.

McNeill, W. H. 1993. Plagues and Peoples. 2^nd ed. New York: Monticello.

Morris, I. 2014. War! what is it Good For?: Conflict and the Progress of Civilization from Primates to Robots. New York, NY: Farrar, Straus and Giroux.

Nefedov, S. A. 2001. Method of Demographic Cycles. Ural'skiy istoricheskiy vestnik 7: 93–107. Original in Russian. (Нефедов, С. А. Метод демографических циклов. Уральский историко-торический вестник 7: 93–107).

Nefedov, S. A. 2002a. A Model of Demographic Cycle. Informatsionniy bulleten' assotsiatsii ‘Istoriya I kompyuter’ 29: 131–142. Original in Russian (Нефедов С. А. Модель демографического цикла. Информационный бюллетень ассоциации «История и компьютер» 29: 131–142).

Nefedov, S. A. 2002b. On the Theory of Demographic Cycles. Ekonomicheskaya istoriya 8: 116–121. Original in Russian (Нефедов С. А. О теории демографических циклов. Экономическая история 8: 116–121).

Nefedov, S. A. 2003. Theory of Demographic Cycles and Social Evolution of Ancient and Medieval Societies of the East. Vostok 3: 5–22. Original in Russian (Нефедов С. А. Теория демографических циклов и социальной эволюции древних и средневековых обществ Востока. Восток 3: 5–22.).

Nefedov, S. A. 2004. A Model of Demographic Cycles in a Traditional Society: the Case of Ancient China. Social Evolution & History 3 (1): 69–80.

Nefedov, S. A. 2005. Demographic and Structural Analysis of Social and Economic History of Russia. The End of the 15^th – the Beginning of the 20^th Century. Ekaterinburg: UGGU Publishing House. Original in Russian (Нефедов С. А. Демографический и структурный анализ социально-экономической истории России. Конец 15 – начало 20 века. Екатеринбург: Издательство УГГУ).

Nefedov, S. A. 2007. Concept of Demographic Cycles. Ekaterinburg: EGGU. Original in Russian (Нефедов С. А. Концепция демографических циклов. Екатеринбург: ЕГГУ).

Nefedov, S. 2008. Factor Analysis of the Historical Process. Moscow: Territoriya buduschego, Original in Russian (Нефедов С. А. Факторный анализ исторического процесса. М.: Территория будущего).

Nefedov, S. A. 2013. Modeling Malthusian Dynamics in Pre-Industrial Societies. Cliodynamics 4 (2): 229–240.

Roberts, N. 1998. The Holocene: An Environmental History. Oxford: Blackwell.

Turchin, P. 2003. Historical Dynamics: Why States Rise and Fall. Princeton: Princeton University Press.

Turchin, P. 2005. War and Peace and War: Life Cycles of Imperial Nations. New York: Pi Press.

Turchin, P. 2007. Historical Dynamics. On the Way to Theoretical History. Moscow: Komkniga/URSS. Original in Russian (Турчин П. В. Историческая динамика. На пути к теоретической истории. М.: ЛКИ/URSS).