Resistance to Socio-Political Instability as an Indicator of the Country's Successful Development

One of the most important indicators of a country's successful development is the resistance of the state and society to socio-political instability coming both from internal and external destructive forces. The destabilization can manifest in the emerging protest movements, extremist views, fundamentalist organizations, nationalism, etc. The relevance of the analysis of country's resistance to socio-political destabilization increases due to the fact that nowadays numerous attempts are made to undermine the political situation in many regions of the world, including in Russia, via soft power. Accordingly, there is a growing need in a scientific interpretation of logic processes of political instability in society in order to resist the possible instability.

The report describes the logical-mathematical model designed to: – Analysis and computer modeling of the sustainable socio-political struc-tures; – The timely identification of risks of social and political instability; – The research of possible ways to overcome them.

The model is verified on historical material (the history of Russia, Great Britain, and France) and used to simulate the specific situations of social and political destabilization (contemporary events in the Middle East, Ukraine, separatist movements in several countries).

Keywords: mathematical modeling, socio-political systems, chaos and destabilization, synchronization, forecasting, risk management.

Social systems are the amalgamations of actors (individuals and legal entities), which on the one hand, have different interests (which show their subjectivity), and on the other hand, when making decisions they have to take into account each other's interests, and to negotiate and mutually coordinate the actions (only in this case one can speak about the existence of a single social system).

The actors can affect each other through a number of different mechanisms: through a system of rules and regulations, through bilateral and multilateral agreements, by coercion, etc. As a result of the interaction, the decisions may converge or synchronize (while the interests remain different); in this case the actors act in a consistent way and social system functions as a single organism. However, if no synchronization of solutions takes place, there will be a disagreement among actors and the system becomes unstabe.

Thus, the aim of the present article is to identify the patterns and intensity of actors' mutual influence which can lead to the emerging consistency of their decisions and actions (not opinions) aimed at supporting a stable functioning of social system.

The information field theory can help to solve this problem (see e.g., Bukharin, Kovalev, and Malkov 2009; Bukharin and Malkov 2010, 2011, 2014), since its conceptual field comprises three quantitative indicators of synchronization or desynchronization of the actors' positions i and j in the decision-making process on a particular issue (the indices take values in the interval between 0 and 1 while the value of zero means a complete consistency, and the value of one – a complete disagreement). Indicators are the following:

• the index of disagreement of opinions So_ij (IDO), which is always above zero;

• the index of disagreement of solutions Ss_ij (IDS), which can be above zero;

• the index of disagreement of actions Sa_ij (IDA), which should tend to zero in social systems.

Let us give an example. IDO reflects the difference of opinions on various issues between the Communist party and the party ‘United Russia’ in the Russian State Duma; IDS reflects the results of voting of the Communist party and the ‘United Russia’ in the State Duma on various laws; IDA characterizes the execution of the adopted laws by the members of both parties.

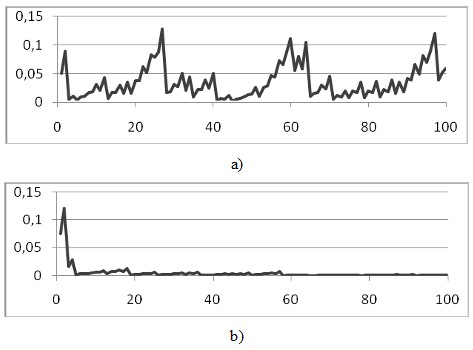
Fig. 1. The typical view of the index disagreement at different moments of time t: a) the situation is a significant disagreement, and b) the situation is almost complete consistency (on the horizontal axis – the value of t, on the vertical axis – the value of S_ij)

The method of assessing the indices of disagreement was developed basing on analogies with the assessment of synchronization of related nonlinear dynamical systems with discrete time (see e.g. Dmitriev, Starkov and Shirokov 1996; Malkov 1998, 2007, 2009; Malkov and Bilyuga 2015).

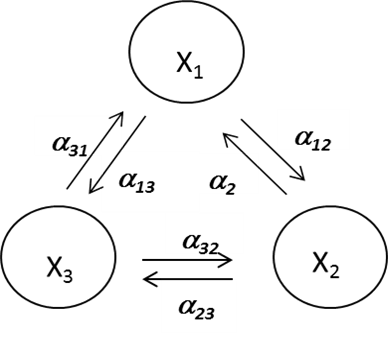
Fig. 2. Synchronization of three connected systems whose dynamics are described by a discrete map F(x(t)) with the Lyapunov exponent λ >0 (λ characterizes the difference of interests):

x₁(t+1)= F((1-a₂₁-a₃₁)∙x₁(t)+ a₂₁∙x₂(t)+ a₃₁∙x₁(t)),

x₂(t+1)= F(a₁₂∙x₁(t)+ (1-a₁₂-a₃₂)∙x₂(t)+ a₃₂∙x₁(t)),

x₃(t+1)= F(a₁₃∙x₁(t)+ a₂₃∙x₂(t)+ (1-a₁₃-a₂₃)∙x₁(t)).

The findings of investigation of chaotic synchronization systems are the following:

– synchronization can occur only when the intensity exceeds a certain threshold value a' (‘synchronization threshold’). Thus, the more chaotic system, the higher the value a' and the stronger must be the connection a_ij to prevent a desynchronization of system (a_ij – is the link between the systems);

– in general, the increasing number of links reduces the synchronization threshold. However, there may be situations when the introduction of new ties in addition to the existing ones does not improve but worsens the synchronization of system dynamics. The ties are not equal and the result of their interaction depends significantly on the overall structure of ties within the system as well as on the value of λ;

– within a certain structure of relations one can increase their intensity to achieve synchronization at any value of λ. However, there are situations when sufficiently large values of λ prevent synchronization regardless of any intensity of a_ij.

At the next stage of the research it was necessary to project this method to the state. It was assumed that a state can be presented as a system of relations between central authorities, local governments, and population. When verifying the assumption on historical data (the case studies were history of France, Germany, Great Britain, the Russian Empire, and Russia) in order to identify the meaningful patterns, we discovered two distinct and sustainable systems of government with high efficiency, namely, the adaptive system (or a democratic republic) and the directory system (or a rigid authoritarian regime). We also suggest that the transition from one system of government to another is rather complicated and accompanied by social instability.

Below we give some examples of highly efficient systems of government.

Fig. 3. Option 1. A rigid directive system of governance (X₁ – Central authorities, X₂ – local governments, X₃ – object of management)

Characteristics: a rigid vertical power structure with weak or absent inverse links. The synchronization threshold is high.

Examples: absolute monarchy, oriental despotism, dictatorship, and totalitarian regime.

The synchronization threshold of system is the following:

a'= a₁₂ + a₂₃= 2 × (1- exp(-l)),

where λ characterizes the difference of interests of main social groups.

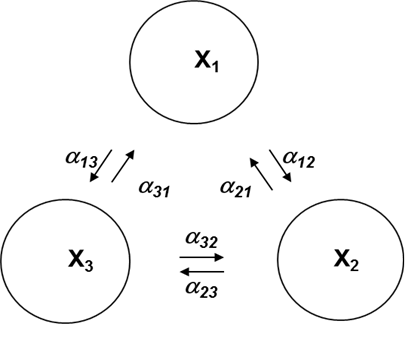
Fig. 4. Option 2: the adaptive control system (X₁ – central authorities, X₂ – local governments, X₃ – object of management)

Characteristics: all ties are involved. The synchronization threshold is low.

Examples: a democratic regime, a parliamentary republic.

The threshold of synchronization system is as follows:

a' = a₁₂+ a₁₃+ a₂₁+ a₂₃ = 4 · a = 4 · (1- exp(-l))/3.

Now let us pass to alternative systems of government with reduced efficiency.

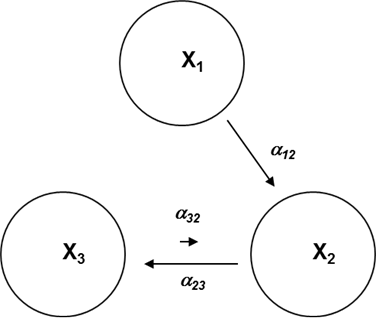
Fig. 5. Option 3: direct system of government with additional inverse links a₃₂ (X₁ – central authorities, X₂ – local governments, X₃ – object of management)

Characteristics: in addition to rigid vertical governance there is imposed a partial local economic independence and elements of self-government. The synchronization threshold increases compared to the original system of the directive system:

To preserve the governability it is necessary to strengthen control actions.

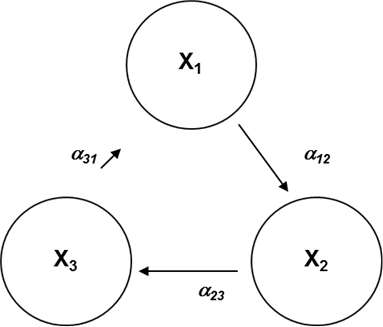
Fig. 6. Option 4: the directive system with additional tie a₃₁ (X₁ – the central authorities, X₂ – local governments, X₃ – object of management)

Characteristics: people's direct influence on the central authorities proceeds through elections, demonstrations, etc. The synchronization threshold reduces if the chaotic rate is low in system, and increases if chaotic rate is high. In the first case, the controllability increases while in the second case it decreases and it is possible to lose the full of control, regardless the intensity of the control actions a₁₂ and a₂₃.

The analysis of the simulation results brings to the following conclusions:

– in authoritarian systems it is necessary to reduce λ (involving ideology and religion as important factors);

– the transition from the authoritarian to adaptive system of government (an imitative democracy) is accompanied by a weakening of the regime;

– this determines the efficiency of ‘soft power’ (the ‘color revolutions’, etc.).

In Fig. 7 we present a possible rational transition from directive system of government to an adaptive system (through strengthening the ties) without a significant reduction of political stability in a society.

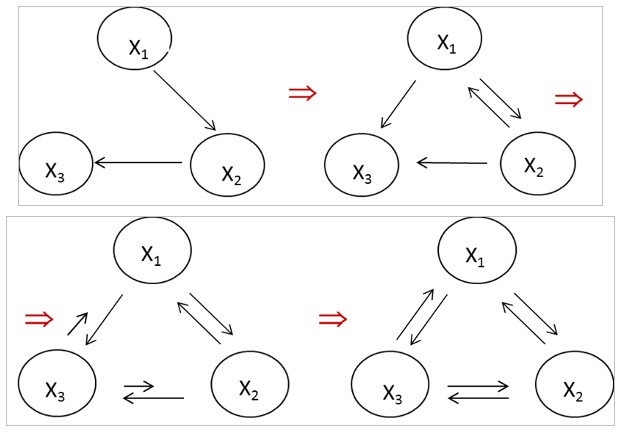
Fig. 7. The rational transition from directive system of government to adaptive system (X₁ – central authorities, X₂ – local governments, X₃ – object of management)

Using the mentioned tool for the analysis of political stability in a society, one can set the task to develop a methodology to forecastthe synchronization/desynchronization of multi-agent social systems.

At the early stages of our research we considered systems consisting of small number of agents in order to compare the simulation results with the actual current events (real events are the events in Ukraine and Novorossia from November 2013 to the present time). The scheme of interaction between the actors in Novorossia conflict is shown in Fig. 8.

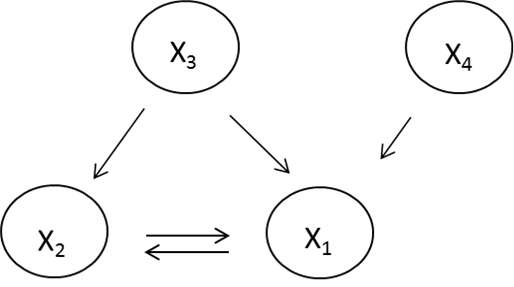
Fig. 8. The scheme of interaction between actors of the conflict in Novorossia: X₁ – Ukraine; X₂ – Novorossia; X₃ – Russia; X₄ – the USA and the EU

Fig. 9 shows the calculated intensity of the USA and the European Union's impact (the values on the y-axis, in relative units) which led to destabilization of the relations between the central Ukrainian authorities and Novorossia with varying intensity of Russia's efforts to stabilize the situation (the values on the x-axis, in relative units) for two cases when initially Ukraine and Novorossia are ready to negotiate (a) and not ready to negotiate (b).

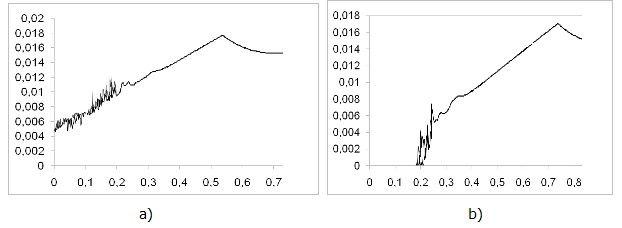
Fig. 9. The results of calculated minimal values of external influences from the USA and the EU (y-axis), which affect the synchronization of the subjects X₁ and X₂ for a given fixed connections between them ((a) – the high level of relationships, (b) – the low level of relations) and various efforts to stabilize the situation from Russia (the x-axis)

Fig. 9 shows that even the Western rather low-intensity desynchronizing impact on Ukraine can bring destabilization (the area above the curve is the area of destabilization). This illustrates the efficiency of soft power tools.

References

Bukharin, S. N., Kovalev, V. I., and Malkov, S. Yu. 2009. To the Formalization of the Concept of Information Field. Informatsionnye voiny 4(12): 2–9. In Russian (Бухарин С. Н., Ковалев В. И., Малков С. Ю. О формализации понятия информационного поля. Информационные войны 4(12): 2–9).

Bukharin, S. N., and Malkov, S. Yu. 2010. On the Question about the Mathematical Modeling of Information Interactions. Informatsionnye voiny 2(14): 14–20. In Russian (Бухарин С. Н., Малков С. Ю. К вопросу о математическом моделировании информационных взаимодействий. Информационные войны 2(14): 14–20).

Bukharin, S. N., and Malkov, S. Yu. 2011. Information Field and the Problem of Choice. Informatsionnye voiny 2(18): 36–45. In Russian (Бухарин С. Н., Малков С. Ю. Информационное поле и проблема выборa. Информационные войны 2(18): 36–45).

Bukharin, S. N., and Malkov, S. Yu. 2014. The Evolution of the Elite. Materials and Research. Moscow: Academic project; Gaudeamus. In Russian (Бухарин С. Н., Малков С. Ю. Эволюция элиты. Материалы и исследования. М.: Академический проект; Гаудеамус).

Dmitriev, A. S., Starkov, S. O., and Shirokov, M. E. 1996. Synchronization of Ensembles of Coupled Maps. Izvestiya vuzov. Applied Nonlinear Dynamics 4(4–5): 40–57. In Russian (Дмитриев А. С., Старков С. О., Широков М. Е. Синхронизация ансамблей связанных отображений. Известия вузов. Прикладная нелинейная динамика 4(4–5): 40–57).

Malkov, S. Yu. 1998. Politics in Terms of Synergetics. Strategic Stability 3: 90–99. In Russian (Малков С. Ю. Политика с точки зрения синергетики. Стратегическая стабильность 3: 90–99).

Malkov, S. Yu. 2007. The Dynamics of Political Systems: Modeling Stability and Destabilization. Informatsionnye voiny 2: 11–20. In Russian (Малков С. Ю. Динамика политических систем: моделирование устойчивости и дестабилизации. Информационные войны 2: 11–20).

Malkov, S. Yu. 2009. Social Self-Organization and the Historical Process: Mathematical Modeling Potentials. Moscow: Publishing House ‘LIBROKOM’. In Russian (Малков С. Ю. Социальная самоорганизация и исторический процесс: Возможности математического моделирования. М.: Книжный дом «ЛИБРОКОМ»).

Malkov, S. Yu., and Bilyuga, S. Ye. 2015. Model of Stability/Destabilization of Political Systems. Informatsionnye voiny 1(33): 7–18. In Russian (Малков С. Ю., Билюга С. Э. Модель устойчивости/дестабилизации политических систем. Информационные войны 1(33): 7–18).