Mathematical Model of Interaction between Civilization Center and Tribal Periphery: A Description

Authors: Korotayev, Andrey; Grinin, Leonid; Grinin, Anton L.
Journal: Social Evolution & History. Volume 20, Number 2 / September 2021

DOI: https://doi.org/10.30884/seh/2021.02.03

This article offers a mathematical model describing the influence of one of the major factors of the World System's macrodynamics throughout most of its history (since the ‘urban revolution’) – the interaction between civilizations and their tribal peripheries. The proposed mathematical model is intended to describe the possible influence of the interaction between the World System civilizational core and its tribal periphery on the formation of the specific curve of the world urbanization dynamics. It simulates completion of the phase transition, behavior of the system in the attraction basin and beginning of the phase transition to the attraction basin of the new attractor and is aimed at identifying the role of the factor of interaction between the civilizational core and barbarian periphery in the formation of attractor effect during the completion of phase transition, that is for clarification of the reasons why there was observed not only the slowdown of growth rates of the main indicators of the World System development after completion of phase transitions during its development, but also their falling with the subsequent temporary stabilization near some equilibrium level.

Keywords: world history, dynamic modeling, the World System, civilizations, tribal periphery, urbanization, asabiyyah, technology, warfare.

Andrey V. Korotayev, HSE University and Lomonosov Moscow State University more

Leonid E. Grinin, HSE University and Institute of Oriental Studies, Russian Academy of Sciences more

Anton Grinin, Lomonosov Moscow State University more

For many millennia, the interaction between civilizations and their peripheries was one of the most important factors leading to the formation of the modern World System (see Part 1 of the Supporting Online Materials1 for detail). The emergence and development of the world urban network was one of the main components of the World System's evolution that accelerated its development and increased its integration.²

Our previous research (Korotayev 2006c, 2007a, 2007b; Korotayev, Komarova, and Khaltourina 2007: 169–177; Grinin, Korotayev 2009b; Korotayev, Grinin 2012, 2013; Grinin 2017a, 2017b) has shown that the curve describing the dynamics of the world urban population has a rather peculiar form (see Figs. 1 and 2).

Three rather distinct periods of relatively fast world urban population growth can be singled out here: A1, from the mid-fourth millennium BCE to the mid-third millennium BCE; A2, the first millennium BCE (roughly corresponding to the ‘Axial Age’); and A3, the nineteenth–twenty-first centuries CE. Moreover, two periods of relatively slow growth of the world urban population (including long phases when the urban population and the world urbanization level would hardly grow or could even considerably fall) can be noted: B1, from the mid-third millennium BCE to the late second millennium BCE; and B2, between the second and seventeenth centuries CE. Two other periods are essentially close to these epochs: Period B0, immediately preceding the mid-fourth millennium (when the world urban population did not grow simply because cities had not yet emerged and no cities existed on the Earth), and Period B3, which is expected to begin in the twenty-second century, when forecasts predict the world urban population will again stop growing in any significant way (since the World System urbanization is supposed to reach its saturation level with stabilization [or even some decline] of the world population) (see, e.g., Korotayev, Malkov, Khaltourina 2006a, 2006b, 2007; Korotayev, Komarova, Khaltourina 2007; Korotayev 2008, 2009, 2012, 2013; Grinin 2006; Korotayev 2018, 2020b).

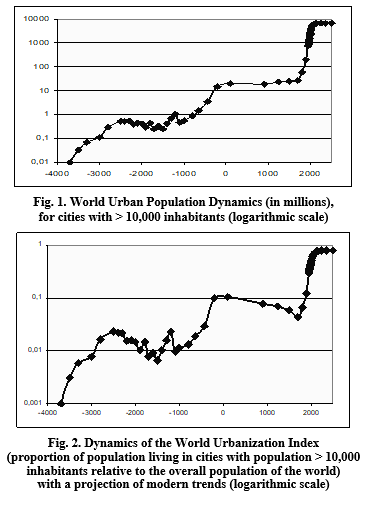
Note that the detected dynamics of world urbanization correlates rather well with the dynamics of the World System political organization (Grinin, Korotayev 2006; Korotayev, Grinin 2006, 2012, 2013; Grinin 2016a, 2016b; Grinin, Ilyin, Andreev 2016). Moreover, the abovementioned synchronous phase transitions to the new levels of the world urbanization and new complexity³ levels of the World System's political organization temporally coincide with phase transitions to higher levels of the World System's political centralization detected by Taagepera, which took place, according to his calculations, during periods А1, А2 and А3 (Taagepera 1997: 485). They also correspond to the phase transitions in global cultural complexity detected by Turchin et al. (2018).

Similar phase transitions appear to be observed in the macrodynamics of world literacy level. In fact, during Period A1, we observe the emergence of the first literate people, whose share in the world population by the end of this period reached the level of decimals of a percent and fluctuated at this level during Period В1. This correspondence is no coincidence; although literate people could be found outside cities, their number in cities was incomparably larger than in rural areas. During Period А2, the world literacy rate grew by an order of magnitude and amounted to several percent of the world's total population; it fluctuated at this level during Period B2 through the mid-eighteenth century, when Period A3 started. During that period, the world literacy level reached a level on the order of dozens per cent, and by the beginning of Period B3 (presumably in the twenty-second century) it is likely to stabilize at the hundred-percent level (see, e.g., Korotayev 2006d; Korotayev, Malkov, Khaltourina 2006a, 2006b).

In fact, the phase transitions mentioned above can be regarded as different aspects of a series of unified phase transitions: Phase Transition A1, from medium complexity agrarian societies to complex agrarian ones; Phase Transition A2, from complex agrarian societies to supercomplex ones; and, finally, Phase Transition A3, from supercomplex agrarian societies to postindustrial ones (from this perspective, the period of industrial societies is a period of phase transition, В2–В3). These phase transitions are also exceptionally strongly connected with production revolutions and transitions from one principle of production to another (for more detail, see Grinin 2007а, 2007b; Korotayev, Grinin 2006). The period of the first attractor (the first phase), in particular, is connected with the first version of the intensive phase of agrarian revolution (transition to irrigation agriculture), whereas the second attractor / phase is connected with the second version of the intensive phase of agrarian revolution (transition to intensive plow non-irrigation agriculture). From the sixteenth to the first half of the twentieth century (especially the nineteenth – the first half of the twentieth century) the phase transition was connected with the transition to the industrial principle of production. The period from the end of the twentieth century and (presumably) the whole twenty-first century is connected with the transition to scientific and information / cybernetic principle of production (for more detail see Grinin 2006; Grinin L., Grinin, A., Korotayev 2017a, 2017b, 2020a, 2020b).

The proposed mathematical model aims at analyzing the possible impact of the interaction between the World System's civilizational core and its tribal periphery on the formation of a curve of the world urbanization dynamics. It describes the completion of the phase transition, the system's behavior in the basin of attraction, and the start of the phase transition to a new basin of attraction. This model also identifies the role of the interaction between civilizational cores and tribal peripheries in the formation of the attractor effect during the completion of phase transition. In other words, we try to determine why, after the phase transitions were completed, a slowdown was observed in the growth rates of the main indicators of the World System development, as well as their decline, with subsequent temporary stabilization at some equilibrium level (note that the model offered cannot describe the fluctuations observed at the respective levels).

Note that the ‘tribal’ periphery can also denoted as ‘barbarian’, following Lewis H. Morgan (1877), where, incidentally, this term is devoid of any pejorative implications (note that Morgan himself in no way despised the ‘barbarians’ – he, in company with Friedrich Engels [1884/1978] – rather admired them). However, we have mostly avoided using this rather appropriate term for the sake of ‘political correctness’.

As is known, there are great differences in the definition of civilization (see, e.g., Grinin 1997, 1998a, 1998b; Grinin, Korotayev 2009: Introduction). In this paper, we operationalize the civilization or civilizational core (center) of the World System as the societies of the World System core with urban settlements; while the peripheral communities without urban settlements are defined as ‘tribal’. Within the framework of the present mathematical model the existence of cities is assumed to be the only formal characteristic of civilization.⁴

Elsewhere we have already analyzed the possible role of interaction between the civilizational core and tribal periphery (see Korotayev, Malkov, Khaltourina 2007: 189–208; Grinin 2003, 2004, 2011; Grinin, Korotayev 2013, 2014, 2018; Grinin et al. 2004) and considered the reasons behind the essential decline (up to negative values) in growth rates of the main indicators of the World System development in the first millennium CE after the completion of А2 phase transition to supercomplex agrarian societies (Korotayev, Malkov, Khaltourina 2006b; Zinkina, Ilyin, Korotayev 2017). Note that the above-men-tioned analysis allowed identification of that factor as one of the very important causes (though not the only one) of the phenomenon considered.

Thus, we have come to the following preliminary conclusions:

The fact that the regime of hyperbolic growth changed after the World System's political centralization had reached critically high level of hyperbolic rates (in the early 1^st millennium CE the absolute majority of World System's inhabitants turned out to be under control of only four empires – Roman, Parthian, Kushan and Han) is not accidental also for some other reasons. The rapid growth of political centralization in the 1^st millennium BCE was driven by the diffusion of iron metallurgy (for more detail see Grinin, Korotayev 2009: Ch. 6; Korotayev, Zinkina 2017; Zinkina, Ilyin, Korotayev 2017), which not only considerably increased the Earth's carrying capacity, but also led to the development of production of rather cheap and effective weapons which promoted the formation of numerous armies without which the emergence of the world empires would be almost impossible. However, this process had important side effects. The politically centralized systems quite often secure military superiority through the development of specialized military subsystems – rather small but well trained and professional armies. However, to preserve this superiority there is necessary to have monopoly on certain effective types of weapons (war chariots, bronze weapons, etc.). If the revolution in production of means of violence takes place and the monopoly on them cannot be efficiently supported (e.g., in case of emergence of iron weapons), the less politically centralized societies with a high proportion of military active population get considerable advantage and in military terms can become stronger than politically centralized societies. This was the case in many parts of Oecumene of the Old World in late antiquity. Moreover, less politically centralized societies with a greater share of military active population could considerably increase their military efficiency without noticeable increase in their political centralization or internal differentiation, for example, through nomadization, growth of specialization on herding since the herder's everyday work and the character of his socialization make him a combat-effective warrior. Nomadic animal husbandry with a widespread use of herders-riders could considerably increase military potential of such societies without additional political centralization and functional differentiation. In this context it is important for us that the side effect of the technological shifts of the first millennium BCE was strengthening of the barbarian periphery's military potential in general and nomadic socio-political systems, in particular... As a result, the nomads got a consistent military superiority over the settled societies throughout most part of the ‘Junior Hyperbole’ epoch (additionally strengthened by the invention and diffusion of stirrups and sabers); this led to an additional reduction in the World System's demographic growth rates not only due to mass depopulations resulting from recurring nomadic invasions, but also as a result of some decrease in the Earth's carrying capacity in many important zones of the World System due to the pressure of barbarian (and, in particular, nomadic) peripheries (here we could recollect the Russian ‘bread-basket’ – Black Earth region which through the most part of the 2^nd millennium was known as the Wild Field since the lands in this region were almost not cultivated because of the threat of nomadic raids) (Korotayev, Malkov, Khaltourina 2007: 207–208).

Here, we present the model founded on the ideas described above, as well as in Part 1 of the Supporting Online Materials, and on our earlier general models of development of the World System (Korotayev 2005, 2006c, 2006d, 2007a, 2008, 2009, 2012, 2013, 2018, 2020b; Korotayev, Malkov, Khaltourina 2006a, 2007; Korotayev, Malkov 2012, 2016; Korotayev, Zinkina 2017; Grinin 2006, 2007a, 2011; Grinin, Grinin 2016) and some ideas of the theory of dynamics of collective solidarity (asabiyyah)⁵ formulated by Peter Turchin (2003, 2005, 2007).

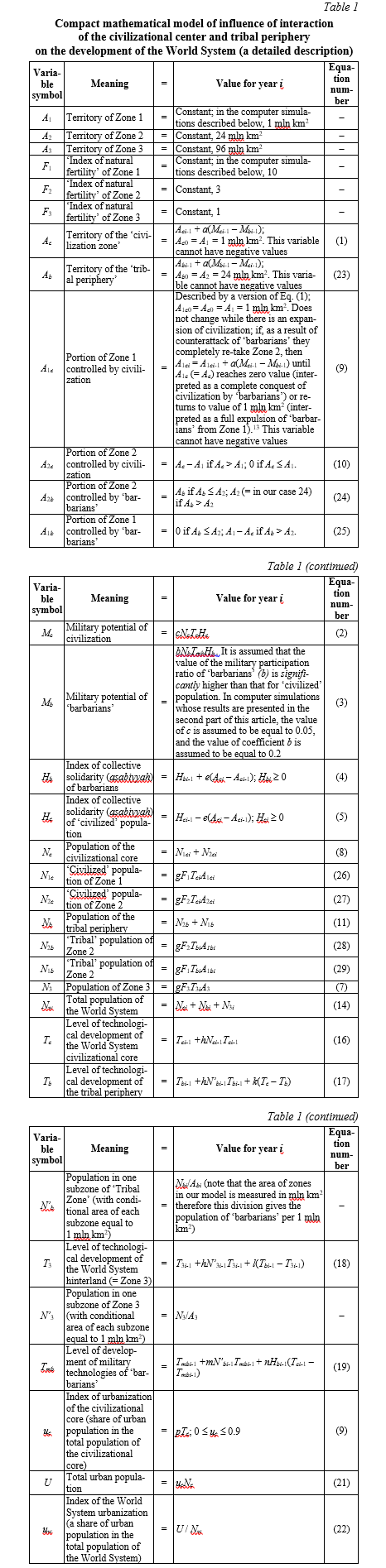
In the proposed model, the World System is assumed to be divided into three main geographical zones: (1) a small (1 mln km²) and highly productive zone; (2) a larger zone with average production capacity (24 mln km²), surrounding Zone 1; and (3) the largest (96 mln km²) and least productive zone, surrounding Zone 2 (Fig. 3).

It can be assumed that the first cities originated in Zone 1 (see, e.g., Korotayev, Grinin 2006, 2012, 2013; Grinin, Korotayev 2009a, 2009b), which can therefore be identified as the ‘civilizational center’. It is assumed that the initial level of technological development in this center (T_c0) is significantly higher than that for the tribal periphery (T_b0) coinciding with Zone 2 at the start of computer simulation. At this point, Zone 3, with the lowest initial level of technological development (T_h0), is considered the World System's hinterland.

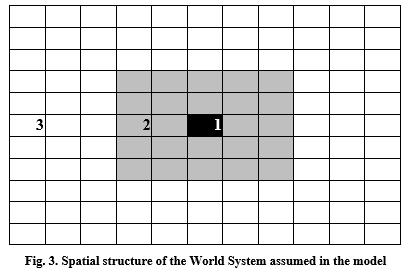
At the first stage of computer simulation the model's basic scenario describes the initial vigorous territorial expansion of the civilizational center supported by its more developed technologies, which, in combination with significantly denser population of the civilization zone, results in a significantly higher military potential. In the proposed model, the civilization's territorial dynamics are mathematically described by means of the following differential equation:

where A_c is the territory controlled by the civilizational core; M_c is the military potential of the civilizational core; M_b is the military potential of tribal periphery; and a is the constant which determines the rate of transformation of military superiority into territorial acquisitions (the calculation pattern for M_c and M_b values will be described below, see Equations (2) and (3)).

However, this expansion is eventually exhausted in the basic scenario of the model and the tribal periphery's counterattack unfolds. Note that in the suggested model (as well as in historical reality) less numerous and technologically backward ‘barbarians’ can put pressure on more numerous and technologically advanced ‘civilized’ enemies. This effect may be produced by the following factors:

1) A higher military participation ratio that was characteristic of ‘barbarians’, as proven by written, ethnographic and even archaeological sources. For example, in some territories occupied by the German tribes before the Great Migration epoch, about 80 per cent of males were buried with iron weapons (see Gurevich 1999: 44). One should also mention the early military training for boys common among many tribal (especially nomadic) peoples, for example, Huns, Mongols or Turks when they were nomads (see, e.g., Nefedov 2008).

The most important role of this factor in explaining the cases of successful advance of the ‘barbarian’ periphery on civilizational center was described in the sixteenth century by the Ethiopian monk Bahrey in his well-known History of the Galla. Bahrey tried to explain why the politically centralized Ethiopian state was constantly defeated by the politically less centralized and less developed Galla (Oromo) tribes (‘How is it that the Galla defeat us though we are numerous and well supplied with arms?’ Bahrey 1976 [1593]: 140). The answer which Bahrey proposed is very interesting and convincing: just because the Ethiopian society was much more developed and socially differentiated (i.e., actually more ‘civilized’), it suffered continuous defeats in the fight against less developed ‘barbarians’, the Galla. In this case the high level of internal differentiation (‘civilization’) becomes a source of military weakness.

How is it that the Galla defeat us, though we are numerous and well supplied with arms? It is because our nation is divided into ten classes, nine of which take no part whatever in war, and make no shame of displaying their fear; only the tenth class makes war and fights to the best of its ability. Now, although we are numerous, those who can fight in war are few in number, and there are many who do not go to war. Of these classes, the first is that of the monks, of whom there are vast numbers. Among them are those who become monks at an early age, drawn thereto by the other monks while they are studying, as indeed was the case with him who has written this history, and others like him. There are also others who become monks because they fear war. A second group is composed of those who are called dabtara, or clerks; they study the holy books and all works relating to the occupations of the clergy; they clap their hands and stamp their feet during divine service, and have no shame for their fear of going to the wars. These people take as their models the levites and priests, namely, the sons of Aaron. The third group is that of the people called Jan Hasana and Jan Maasare, who look after the administration of justice, and keep themselves from war. The fourth group is formed by those who escort the wives of dignitaries and the princesses; they are vigorous, brave, and strong men who nevertheless do not go to war, for they say, ‘We are the protectors of the women’. The fifth group calls itself ema gelle, ‘elders’; they are the lords and hereditary landowners: they share their land with their laborers, and are not ashamed of their fear. The sixth group is that of the laborers in agriculture, who live in the fields and have no thought of taking part in war. The seventh group is composed of those who engage in trade and gain profit thereby. The eighth group is that of the artisans, such as the smiths, scribes, carpenters, and such-like, who know not the art of war. The ninth group is that of the wandering singers, those who play the qanda kabaro [a small drum] and the bagana, whose profession is to beg, to collect money. They invoke blessings on those who reward them, flattering them with vain praises and idle panegyrics; while those who refuse to give them presents they curse, though they are not blameworthy for this, for, as they say, ‘This is our custom.’ Such people keep themselves as far as possible from war. The tenth group, finally, is composed of those who carry the shield and spear, who can fight, and who follow the steps of their king to war. It is because these are so few in number that our country is ruined. Among the Galla, on the contrary, these nine classes which we have mentioned do not exist; all men, from small to great, are instructed in warfare, and for this reason they ruin and kill us (Bahrey 1976 [1593]: 140–141).

In our model, the higher coefficient of military participation that was typical for ‘barbarians’ is mathematically described in Equation (3) by giving coefficient b (representing the military participation ratio of ‘barbarians’ here, i.e., the percentage of tribal population participating in military operations) a significantly higher value than that of coefficient c (representing the military participation ratio for the ‘civilized’ population) in Equation (2). For example, in the computer simulations (whose results will be presented in our next article) for the main scenario of our model, the value of с is 0.05, whereas the value of b is 0.2.

where N_b is the number of inhabitants of the tribal periphery; T_mb is the level of development of military technologies in the tribal periphery (it is assumed that this variable is not identical with the general level of technological development of the tribal periphery; the implications of this assumption will be considered below); and H_b is the level of barbarians' asabiyyah.

2) Borrowing of military technologies by ‘barbarians’ happened at higher rates than the borrowing of non-military technologies (the way we chose to model this assumption mathematically will be described below). For example, because the Mongols borrowed siege equipment and technology from China, they were able to successfully take many cities. Thus, in this case, borrowing of military innovations was one of important factors leading to mass destruction of cities of the World System in the thirteenth century. Nevertheless, the abovementioned facts about technological borrowing refer not only to weapons, but also to the strategy, tactics, and organization of the army. Quite often, ‘barbarians’ simply imitated the structure of the armies (or separate military institutes) of the neighboring civilizations. For example, the German leader Maroboduus (the late first century BCE – early first century CE), having united Marcomanni with the Lugians, the Mugilones, Ghots and other Germanic tribes, created a large army on the Roman pattern, numbering 70,000 infantry and 4,000 cavalry (SIE 1966: 123).

3) The beginning of forceful expansion of the civilizational core upon the tribal periphery can be interpreted as the formation of a meta-ethnic frontier between the civilization and the tribal world. As clearly demonstrated by Peter Turchin (2003, 2005, 2007), the formation of such a metaethnic border tends to lead to a significant increase in asabiyyah in the party under pressure.⁶ As a result, if at the beginning of its forceful expansion civilization faced scattered groups of ‘barbarians’ incapable of producing any effective resistance, further on, these groups began to cooperate more and more with each other when resisting civilization, and civilization had to deal with more and more united and large coalitions of ‘barbarians’ (which were formed in many respects as a reaction to forceful expansion and were able to show increasingly effective resistance, and even start successful counterattacks). Turchin suggests the use of the term asabiyyah, introduced into the scientific discourse by Abd al-Rahman Ibn Khaldun⁷ (1332–1406), to denote ‘collective solidarity’.⁸

In the model, the dynamics of tribal asabiyyah (H_b) is described mathematically by means of the following equation:

where e is a constant. It means that the higher the rates of forceful territorial expansion of civilization, the higher the growth rates of barbarians' asabiyyah.⁹

Respectively:

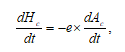
where H_c is asabiyyah of civilized population.

Note that it means that asabiyya of civilization begins to grow under the pressure of ‘barbarians’, and the stronger this pressure is, the quicker it grows (see evidence for this in Turchin 2005).

While describing population dynamics, we use the simplified version of the compact model of demographic, technological and economic development of the World System as our basis (Kremer 1993; Korotayev 2005, 2006d, 2007a, 2007b, 2008, 2009, 2012, 2013, 2018, 2020b; Korotayev, Malkov, Khaltourina 2005, 2006a, 2006b, 2007; Korotayev, Malkov S. 2012; Zinkina, Malkov, Korotayev 2014; Korotayev, Malkov A. 2016; Korotayev, Zinkina 2017; Grinin 2012; Grinin L., Grinin A. 2016; Grinin A., Grinin L. 2015; Grinin, Korotayev 2016; Grinin L., Grinin A., Korotayev 2017a, 2020b). We make a Malthusian assumption that throughout most of the period of humankind's existence, the human population was limited by the level of development of life-supporting technologies. As in Kremer's simplified model (1993: 685), we assume that population comes to the technologically determined level of the Earth's carrying capacity instantly (in other words, humankind instantly fills the ecological niche expanded as a result of technological growth).¹⁰ We also take into account the fact that territory with a higher natural productivity can support the existence of a larger population at the same level of technological development than territory with smaller natural producing capacity, and under otherwise equal conditions a larger territory can support a larger population than a smaller territory. Thus, the population size (N) of some zone with productivity F and area A at level of development of life-supporting technologies T will be described mathematically by Equation 6,

where g is a constant.

As a result, the mathematical description of the population for year i for a hinterland of the World System (Zone 3) appears to be the simplest in our model, since we have initially assumed that the territory occupied by it throughout the modeled period remains constant, and the level of technological development is the same for the whole zone:

The situation with the civilizational core and tribal periphery of the World System is a little more complicated. The issue is that throughout the most part of the modeled period the civilization zone is divided into two subzones with different natural productivity, i.e., the core of the civilization zone with high natural productivity (~ Zone 1) and the periphery of the zone corresponding to the part of less productive Zone 2 taken by the civilization from ‘barbarians’. Thus,

Similar to our general model of World System development, the mathematical description of technological dynamics is based upon the equation for technological growth proposed by Michael Kremer¹¹ (Kremer 1993: 686):

where h is a constant (~ coefficient of innovative technological activity of the population).

We assume that the diffusion of innovations proceeds from the civilization center of the World System to its tribal periphery and from there to the hinterland (1). Though in reality the diffusion of innovations from hinterland to periphery (2), from periphery to center (3), and between various subzones of periphery (4) and hinterland (5) was also observed, the main flow of technological diffusion was center–periphery (see, e.g., Chubarov 1991; Grinin A. and Grinin L. 2015), and we decided to refrain from the modeling the diffusion of technological innovations in other directions for the sake of simplicity.

Thus, the following system of difference equations has been used in our model to model the technological development of the World System:

The effect of the most interest for us can be described by means of Eqs. (17) and (19) by giving a higher value to coefficient n in Eq. (19) in comparison with the value of coefficient k in Eq. (17). This equation also describes an assumption that the rates of ‘barbarian’ borrowing of military technologies grows along with the growth of their asabiyyah.

We assume that the entire urban population of the World System is concentrated in its civilizational core. For mathematical description of urbanization dynamics in the model, the following equation is used:

where u_ci is the index of urbanization of the civilizational core (a share of urban population in the total population of civilization core), and p is a constant. The possibility of approximation of u_ci ~ pT follows from the equations of our compact model of the general World System development (Korotayev, Malkov, Khaltourina 2007; Korotayev, Komarova, Khaltourina 2007; Korotayev 2012, 2013). We use the World System Technological Development Index we previously proposed (Korotayev 2006d) for an empirical test of this hypothesis. This index was calculated on the basis of the Hellemans – Bunch database (Hellemans, Bunch 1988). In this database, Hellemans and Bunch tried to record in chronological sequence all the main inventions and discoveries made by the 1980s. As a value of the World System Technological Development Index for moment X, we use the total number of inventions and discoveries made in the World System up to that moment.

The correlation between this World System Technological Development Index and the World System Urbanization Index we previously calculated (Korotayev, Malkov, Khaltourina 2007: 122–127; Korotayev 2007b; Grinin, Korotayev 2009: Ch. 4) is depicted in Fig. 4.

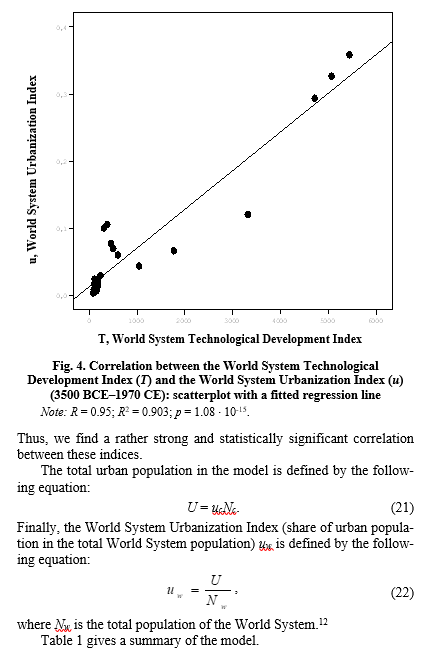
In the second part of this article we will analyze the dynamics generated by this model. It will be shown that interaction between the civilizational center and ‘barbarian’ periphery really can explain some characteristic features of the World System dynamics in the fourth millennium BCE – the second millennium CE.

(to be concluded in the next issue)

ACKNOWLEDGMENTS

This research was performed according to the Development program of the Interdisciplinary Scientific and Educational School of Lomonosov Moscow State University ‘Mathematical methods of analysis of complex systems.’

FUNDING

This research has been supported by the Russian Science Foundation (Project No 20-61-46004).

NOTES

¹ See https://www.sociostudies.org/journal/files/seh/2021_2/supporting_materials.php.

2 Not without reason did V. Gordon Childe focus on the urban revolution (Childe 1952: Chapter 7). It is also quite clear that the processes of functional differentiation, social stratification and class formation proceeded in many ancient agricultural societies under a considerable influence from the ‘urban revolution’ (Alekshin 1986: 22). ‘City’ also implies a complex concentration of geographical, social, political, and sacral resources and assets. ‘The city is a direct territorial concentration of multiple heterogeneous forms of human activities’ (Akhiezer 1995: 23). One can see the closest connection between urbanization, on the one hand, and the formation and development of civilizations and statehood, on the other (see, e.g., Korotayev, Grinin 2006, 2012, 2013; Grinin 2007a; Masson 1989).

3 In this article sociocultural complexity is categorized along the lines outlined in Turchin et al. 2018.

4 The identification of this characteristic as a working criterion of civilization within our mathematical model should, of course, be treated just as an assumption. It is explained by the necessity to determine in an operationalizable way within the present formal / mathematical research the societies forming the World System core and having urban settlements as distinct from peripheral societies (designated here as ‘tribal’/‘barbarian’) lacking those settlements. Let us note that this does not contradict some researchers' rather fair statements that in the context of their research this characteristic can be substituted, for example, by the presence of monumental buildings (see, e.g., Masson 1989).

5 On this term see below for more details.

6 Those who withstood it found responses to the challenge that finally led to the selection of types of tribal communities most adapted to fighting against civilization.

7 See, e.g., Ibn Khaldun 1958, 2004; Alekseev, Khaltourina 2004; Turchin 2003, 2007; Korotayev, Khaltourina 2006; Korotayev 2006a, 2007c, 2007d; Inan 1933; Mahdi 1937.

8 It is a peculiar ideology of tribal solidarity, which allows tribal people to be united into a powerful military force, for example, when putting together groups of tribes. Therefore, Morton Fried (1975) has reason to state that tribes are the secondary non-primitive formations emerging under the influence of neighboring communities with significantly higher level of sociocultural complexity (see also Korotayev 1997a, 1997b, 2000a, 2000b, 2003, 2004, 2006b, 2020a, 2021; Grinin 2007a).

9 We also assume that with the increase in barbarians' asabiyyah the rate of borrowing of military technologies of civilization increases (this assumption is modeled by Eq. (19)). We also assume that variable H cannot have negative values.

10 Let us note that it deprives us of an opportunity to describe cyclical dynamics of the system in the basin of attraction (see, e.g., Korotayev, Malkov, Khaltourina 2006b; Korotayev, Komarova, Khaltourina 2007) that would bring dynamics generated by the model considerably closer to actually observable dynamics. However, this considerably simplifies the suggested model, which made us dwell on this simplified version of description of dependence of population on the level of technological development.

1¹ Note that this equation was also independently proposed by Rein Taagepera (1976, 1979).

1² Thus, the World System urbanization appears here in our model as a purely dependent variable. Perhaps it would make sense to consider its influence on some other key variable models (e.g., on the rates of technological growth, as examined by Artzrouni and Komlos [1985]; in our opinion, their model might allow us to give a more exact description of technological dynamics of the World System in the basins of attraction of attractors B₁ and В₂), but in order to avoid excessive complication of the model we opt to refrain from this, though the action of this factor may be considered in future models.

1³ It is obvious that the easiest way to model the dynamics of this variable is to give it the value of A₁ (1 in our computer simulations) when A_c ³ A₁ and value A_c when A_c < A₁. This method was also applied by us in computer simulations for this and other similar variables (A_2c, A_2b, and A_1b).

1⁴مقدمة ابن خلدون / تأليف عبد الرحمن ابن خلدون. القاهرة: دار الفجر في التراث، 2004.

1⁵ القاهرة: دار الكتب المصرية، 1933. ابن خلدون : حياته و تراثه الفكري / تأليف محمد عبد الله عنان.

REFERENCES

Akhiezer, A. 1995. The City – Focus of the Urbanization Process. In Sayko, E. V. (ed.), City as Sociocultural Phenomenon of Historical Process (pp. 21–28). Moscow: Nauka. Original in Russian (Ахиезер А. С. Город – фокус урбанизационного процесса. Город как социокультурное явление исторического процесса / Ред. Э. В. Сайко, с. 21–28. М.: Наука).

Alekseev, I., Khaltourina, D. 2004. Ibn Khaldun and the Theory of Demographic Cycles in Modern Social Sciences. In Steblin-Kamensky, I. M. et al (eds.), School of the Young Orientalist – 2004 (pp. 129–133). St. Petersburg: St. Petersburg State University. Original in Russian (Алексеев И. Л., Халтурина Д. А. Ибн Халдун и теория демографических циклов в современных социальных науках. Школа молодого востоковеда – 2004 / Ред. И. М. Стеблин-Каменский, и др., с. 129–133. Санкт Петербург: СПбГУ).

Alekshin, V. 1986. Some Regularities of Development of Social System of the Ancient Agrarian Societies (According to Funeral Ceremonies). In Masson, V. M. (ed.), Ancient Civilizations of the East (pp. 21–29). Tashkent: FAN. Original in Russian (Алекшин В. А. Некоторые закономерности развития общественного строя древнеземледельческих обществ (по данным погребальных обрядов). Древние цивилизации Востока / Ред. В. М. Массон, с. 21–29. Ташкент: ФАН).

Artzrouni, M., Komlos, J. 1985. Population Growth through History and the Escape from Malthusian Trap: A Homeostatic Simulation Model. Genus 41: 21–39.

Bahrey. 1976 [1593]. History of the Galla. In Beckingham, C. F., and Huntingford G. W. B. (eds.), Some Records of Ethiopia (1593–1646). London: Hakluyt Society.

Childe, G. 1952. New Light on the Most Ancient East. 4^th ed. London: Rout-ledge.

Chubarov, V. 1991. The Middle Eastearn Locomotive: The Developmental Pace of Technique and Technology in the Ancient World. In Korotayev, A., and Chubarov, V. (eds.), Archaic Society: Main Problems of Sociology of Development. Vol. 1 (pp. 92–135). Moscow: History Institute. Original in Russian (Чубаров В. В. Ближневосточный локомотив: темпы развития техники и технологии в древнем мире. Архаическое общество: узловые проблемы социологии развития / Ред. А. В. Коротаев, В. В. Чу-баров, т. 1, с. 92–135. М.: Институт истории СССР АН СССР).

Engels, F. 1884 [1978]. The Origin of the Family, Private Property and the State. Moscow: Izdatelstvo inostrannoi literatury. Original in Russian (Энгельс Ф. Происхождение семьи, частной собственности и государства. М.: Издательство иностранной литературы).

Fried, M. 1975. The Notion of Tribe. Menlo Park, CA: Benjamin-Cummings.

Grinin, A., and Grinin, L. 2015. The Cybernetic Revolution and Historical Process. Social Evolution & History 14 (1): 125–184.

Grinin, L. 1997. Formations and Civilizations. Ch. 3. Section 4. Filosofiya
i obschestvo 4: 5–62. Original in Russian (Гринин Л. Е. Формации и цивилизации. Глава 3. Философия и общество 3: 5–92).

Grinin, L. 1998a. Formations and Civilizations. Introduction into the Theory of Historical Process. Filosofiya i obschestvo 1: 7–54. Original in Russian (Гринин Л. Е. Формации и цивилизации. Глава 7. Законы исторического процесса. Философия и общество 6: 5–51).

Grinin, L. 1998b. Formations and Civilizations. The Notion of Civilization within the Framework of the Theory of the Historical Process. Filosofiya i obschestvo 2: 5–89; 3: 5–54. Original in Russian (Гринин Л. Е. Формации и цивилизации. Глава 7. Законы исторического процесса. Философия и общество 6: 5–51).

Grinin, L. 2003. The Early State and its Analogues. Social Evolution & History 1: 131–176.

Grinin, L. 2004. The Early State and Its Analogues: A Comparative Analysis. In Grinin, L. E. et al. (eds.), The Early State, Its Alternatives and Analogues (pp. 88–136). Volgograd: Uchitel.

Grinin, L. 2006. Periodization of History: A Theoretic-Mathematical Analysis. In Grinin, L. E., de Munck, V., and Korotayev, A. V. (eds.), History & Mathematics: Analyzing and Modeling Global Development (pp. 10–38). Moscow: KomKniga/URSS.

Grinin, L. 2007a. State and Historical Process. 3 vols. Moscow: URSS. Original in Russian (Гринин Л. Е. Государство и исторический процесс: Политический срез исторического процесса. 3 книги. М.: КомКни-га/URSS).

Grinin, L. 2007b. Industrial Revolutions as the Most Important Thresholds of History. In Kulpin, E. S. (ed.), Human and Nature: Confrontation and Harmony (pp. 191–221). Moscow: IATs-Energiya. Original in Russian (Гринин Л. Е. Производственные революции как важнейшие рубежи истории. Человек и природа: противостояние и гармония / Ред. Кульпин Э. С., с. 191–221. М.: ИАЦ-Энергия).

Grinin, L. 2011. The Evolution of Statehood. From Early State to Global Society. Saarbrücken: Lambert Academic Publishing.

Grinin, L. 2012. Macrohistory and Globalization. Volgograd: Uchitel.

Grinin, L. 2016a. The New World Order and Philosophy. In Chumakov, A. N., and Gay, W. C. (eds.), Between Past Orthodoxies and the Future of Globalization. Contemporary Philosophical Problems (pp. 143–156). Leiden: Brill. URL: http://www.brill.com/products/book/between-past-orthodoxies-
and-future-globalization.

Grinin, L. 2016b. Evolution of the World Order. In Grinin, L. E, and Korotayev, A. V. (eds.), Evolution and Big History: Dimensions, Trends, and Forecasts (pp. 75–95). Volgograd: ‘Uchitel’ Publishing House.

Grinin, L. 2017a. On Systemic Integration in the World System since the Bronze Age. Social Evolution & History 16 (2): 76–111.

Grinin, L. 2017b. The Processes of Systemic Integration in the World System. Journal of Globalization Studies 8 (1): 97–118.

Grinin, L., Carneiro, R., Bondarenko, D. M., Kradin, N. N., and Korotayev, A. (eds.) 2004. The Early State, Its Alternatives and Analogues. Volgograd: Uchitel.

Grinin, L., Grinin, A. 2016. The Cybernetic Revolution and the Forthcoming Epoch of Self-Regulating Systems. Moscow: Moscow branch of Uchitel Publishing House.

Grinin, L., Grinin, A., Korotayev, A. 2017a. Forthcoming Kondratieff wave, Cybernetic Revolution, and Global Ageing. Technological Forecasting & Social Change 115: 52–68.

Grinin, L., Grinin, A., Korotayev, A. 2017b. The MANBRIC-Technologies in the Forthcoming Technological Revolution. In Devezas, T., Leitão, J., and Sarygulov, A. (eds.), Industry 4.0: Entrepreneurship and Structural Change in the New Digital Landscape (pp. 243–261). Heidelberg – New York – Dordrecht – London: Springer.

Grinin, L., Grinin, A., Korotayev, A. 2020a. A Quantitative Analysis of Worldwide Long-Term Technology Growth: From 40,000 BCE to the Early 22^nd Century. Technological Forecasting and Social Change 155: 1–15. https://doi.org/10.1016/j.techfore.2020.119955.

Grinin, L., Grinin, A., Korotayev, A. 2020b. Dynamics of Technological Growth Rate and the Forthcoming Singularity. In Korotayev A., LePoire, D. (eds.), The 21st Century Singularity and Global Futures. A Big History Perspective (pp. 287–344). Cham: Springer.

Grinin, L., Ilyin, I. V., and Andreev, A. I. 2016. World Order in the Past, Present, and Future. Social Evolution and History 15 (1): 58–84.

Grinin, L., Korotayev, A. 2006. Political Development of the World System: A Formal Quantitative Analysis. In Turchin, P., Grinin, L., Korotaev, A., and de Munck, V. (eds.), History and Mathematics. Historical Dynamics and Development of Complex Societies (pp. 115–153). Moscow: KomKniga/URSS.

Grinin, L., Korotayev, A. 2009. Social Macroevolution. Genesis and Transformations of the World System. Moscow: LKI/URSS. Original in Russian (Гринин Л., Коротаев А. Социальная макроэволюция. М.: ЛКИ/УРСС).

Grinin L., Korotayev A. 2009a. The Epoch of the Initial Politogenesis. Social Evolution & History 8 (1): 52–91.

Grinin, L., Korotayev, A. 2009b. Social Macroevolution: Growth of the World System Integrity and a System of Phase Transitions. World Futures 65 (7): 477–506.

Grinin, L., Korotayev, A. 2013. The Origins of Globalization. In Sheffield, J., Korotayev, A., and Grinin, L. (eds.), Globalization. Yesterday, Today, and Tomorrow (pp. 1–29). Litchfield Park, AZ: Emergent Publications.

Grinin, L., Korotayev, A. 2014. Origins of Globalization in the Framework of the Afroeurasian World-System History. Journal of Globalization Studies 5 (1): 32–64.

Grinin, L., Korotayev, A. 2016. Near East, India, and China in Globalization Processes. Moscow: Moscow branch of Uchitel Publishing House. Original in Russian (Гринин Л. Е., Коротаев А. В. Ближний Восток, Индия и Китай в глобализационных процессах. М.: Моск. ред. изд-ва «Учитель»).

Grinin, L., Korotayev, A. 2018. Origins of Globalization in the Framework of the Afroeurasian World-System History. Comparing Globalizations, World-Systems Evolution and Global Futures / Ed. by T. D. Hall, pp. 37–70. Cham:Springer. URL: https://doi.org/10.1007/978-3-319-68219-8_3.

Gurevich, A. Ya. 1999. Ancient Germans. Vikings. In Gurevich, A. Ya., Selected Works. Vol. 1. Moscow – St. Petersburg: Universitetskaya kniga. Original in Russian (Гуревич А. Я. Древние германцы. Викинги. Избранные труды / А. Я. Гуревич. Т. 1. М. – СПб.: Университетская книга).

Hellemans, A., and Bunch, B. 1988. The Timetables of Science. New York, NY: Simon and Schuster.

Ibn Khaldūn, `Abd al-Rahman. 1958. The Muqaddimah: An Introduction to History. New York, NY: Pantheon Books (Bollingen Series, 43).

Ibn Khaldūn, `Abd al-Rahmān. 2004. Muqaddimat ibn Khaldūn. al-Qāhirah: Dar al-Fajr li-l-Turāth.¹⁴

‘Inān, Muḥammad ‘Abd Allāh. 1933. Ibn Khaldūn: ḥayātu-hu wa-turāthu-hu al-fikriyy. al-Qāhirah: Dār al-Kutub al-Misriyyah.¹⁵

Korotayev, A. 1997a. Genesis of Tribal Organization in the North-East Yemen Highlands. In Oriental Studies in the 20th Century: Achievements and Prospects (pp. 194–198). Moscow – Budapest: Russian Orienalists' Association. ICANAS.

Korotayev, A. 1997b. Sabean Studies. Some General Trends and Factors of Evolution of Sabean Civilization. Moscow: Vostochnaya literatura. Original in Russian (Коротаев А. В. Сабейские этюды. Некоторые общие тенденции и факторы эволюции сабейской цивилизации. М.: Восточная литература).

Korotayev, A. 2000a. From State to Chiefdom? From Chiefdom to Tribe? (Some General Tendencies of Evolution of the South Arabian Socio-Political Systems for the Last Three Thousand Years). In Popov, V. A. (ed.), Early Forms of Social Organization. Genesis, Functioning, Historical Dynamics (pp. 224–302). St. Petersburg: Vostochnaya literatura. Original in Russian (Коротаев А. От государства к вождеству? От вождества к племени? (Некоторые общие тенденции эволюции южноаравийских социально-политических систем за последние три тысячи лет). Ранние формы социальной организации. Генезис, функционирование, историческая динамика / Ред. В. А. Попов, с. 224–302. СПб.: Восточная литература).

Korotayev, A. 2000b. Tribe as a Form of Socio-Political Organization of Complex Non-Primitive Societies (Based on Materials of Northeast Yemen). In Kradin, N. N., Korotayev, A. V., Bondarenko, D. M., and Lynsha, V. A. (eds.), Alternative Ways to Civilization (pp. 265–291). Moscow: Logos. Original in Russian (Коротаев А. В. Племя как форма социально-политической организации сложных непервобытных обществ (в основном по материалам Северо-восточного Йемена). Альтернативные пути к цивилизации / Ред. Н. Н. Крадин, А. В. Коротаев, Д. М. Бондаренко, В. А. Лынша, с. 265–291. М.: Логос).

Korotayev, A. 2003. Penetration of Nomads to the Arabian South and Formation of Tribal Organization among the North-East Yemen Agricultural Population. In Kradin, N. N., Bondarenko, D. M., and Th. J. Barfield (eds.), Nomadic Pathways in Social Evolution (pp. 114–122). Moscow: Institute for African Studies.

Korotayev, A. 2004. The Chiefdom: Precursor of the Tribe? In Grinin, et al. 2004 (eds.): pp. 300–325.

Korotayev, A. 2005. A Compact Macromodel of World System Evolution. Journal of World-Systems Research 11 (1): 79–93.

Korotayev, A. 2006a. Long-Term Political-Demographic Dynamics of Egypt: Cycles and Trends. Moscow: Vostochnaya literatura. Original in Russian (Коротаев А. В. Долгосрочная политико-демографическая динамика Египта: циклы и тенденции. М.: Вост. лит-ра).

Korotayev, A. 2006b. Social History of Yemen of the 10^th Century BCE – 20^th Century CE. Moscow: Komkniga/URSS. Original in Russian (Корота-
ев А. В. Социальная история Йемена. М.: КомКнига/URSS).

Korotayev, A. 2006c. The World System Urbanization Dynamics: A Quantitative Analysis. In Turchin, P., Grinin, L., Korotayev, A., and de Munck, V. C. (eds.), History & Mathematics: Historical Dynamics and Development of Complex Societies (pp. 44–62). Moscow: KomKniga/URSS.

Korotayev, A. 2006d. The World System History Periodization and Mathematical Models of Socio-Historical Processes. In Grinin, L., de Munck, V. C., and Korotayev, A. (eds.), History & Mathematics: Analyzing and Modeling Global Development (pp. 39–98). Moscow: KomKniga/URSS.

Korotayev, A. 2007a. Compact Mathematical Models of World System Development, and How They can Help us to Clarify our Understanding of Globalization Processes. In Modelski, G., Devezas, T., and Thompson, W. R. (eds.), Globalization as Evolutionary Process: Modeling Global Change (pp. 133–160). London: Routledge.

Korotayev, A. 2007b. Macrodynamics of the World System Urbanization: A Quantitative Analysis. In Malkov, S., Grinin, L., and Korotayev, A. (eds.), History and Mathematics: Macrohistorical Dynamics of the Society and State (pp. 21–39). Moscow: Komkniga/URSS. Original in Russian (Коротаев А. В. Макродинамика урбанизации Мир-Системы: количественный анализ. История и Математика: Макроисторическая динамика общества и государства / Ред. С. Ю. Малков, Л. Е. Гринин, А. В. Коротаев, с. 21–39. М.: КомКнига/URSS).

Korotayev, A. 2007c. Sociological Theory of Abd al-Rahman ibn Khaldun (1332–1406) as a Methodological Basis for the Mathematical Modeling of Political-Demographic Dynamics of Medieval Еgypt. In Dilek, Z. (ed.), 38. ICANAS. Abstracts (p. 310). Ankara: ICANAS.

Korotayev, A. 2007d. Sociological Theory of Abd al-Rahman ibn Khaldun as a Methodological Basis for the Mathematical Modeling of Long-Term Political-Demographic Dynamics. In Malinetsky, G. G. (ed.), Abstracts of 2^nd International conference Mathematical Modeling of Historical Processes Preprint, Inst. Appl. Math., the Russian Academy of Science (pp. 31–34). Moscow: Institut Prikladnoy matematiki. Original in Russian (Коротаев А. В. Социологическая теория Абд Ар-Рахмана ибн Халдуна как методологическая основа математического моделирования долгосрочной политико-демографической динамики. Тезисы докладов II Международной конференции Математическое моделирование исторических процессов / под ред. Г. Г. Малинецкого. М.: ИПМ им. М. В.Келдыша РАН).

Korotayev, A. 2008. Globalization and Mathematical Modeling of Global Development. In Grinin, L. E., Beliaev, D. D., and Korotayev A. V. (eds.), Hierarchy and Power in the History of Civilizations: Political Aspects of Modernity (pp. 225–240). Moscow: LIBROCOM/URSS.

Korotayev, A. 2009. Compact Mathematical Models of the World System Development and Their Applicability to the Development of Local Solutions in Third World Countries. In Sheffield, J. (ed.), Systemic Development: Local Solutions in a Global Environment (pp. 103−116). Litchfield Park, AZ: ISCE Publishing.

Korotayev, A. 2012. Globalization and Mathematical Modeling of Global Development. In Grinin, L. E., Ilyin, I. V., and Korotayev, A. V. (eds.), Globalistics and Globalization Studies (pp. 148–158). Volgograd: ‘Uchi-tel’ Publishing House.

Korotayev, A. 2013. Globalization and Mathematical Modeling of Global Evolution. In Grinin, L. E., Korotayev A. V. (eds.), Evolution: Development within Big History, Evolutionary and World-System Paradigms (pp. 69–83). Volgograd: ‘Uchitel’ Publishing House.

Korotayev, A. 2018. The 21^st Century Singularity and its Big History Implications: A re-analysis. Journal of Big History II (3): 71–118. http://dx.doi.org/ 10.22339/jbh.v2i3.2320.

Korotayev, A. 2020a. Evolution of Sociopolitical Institutions in North-East Yemen (The 1st Millennium BCE–The 2nd Millennium CE). In Bondarenko, D. M., Kowalewski, S. A., and Small, D. B. (eds.), The Evolution of Social Institutions. Interdisciplinary Perspectives (pp. 161–184). Cham: Springer. DOI: 10.1007/978-3-030-51437-2_7.

Korotayev, A. 2020b. The 21^st Century Singularity in the Big History Perspective. A re-analysis. In Korotayev, A.V., LePoire, D. (eds.), The 21st Century Singularity and Global Futures. A Big History Perspective (pp 19–75). Springer, Cham. https://doi.org/10.1007/978-3-030-33730-8_2.

Korotayev, A. 2021. From Chiefdom to Tribe? Trends in the Evolution of Political Systems in North-Eastern Yemen in the Last Two Millennia. Nouvelles Chroniques du manuscrit au Yémen 32.

Korotayev, A., Grinin, L. 2006. Urbanization and Political Development of the World System: A Comparative Quantitative Analysis. In Turchin, P., Grinin, L., Korotayev, A., and de Munck, V. (eds.), History and Mathematics. Historical Dynamics and Development of Complex Societies (pp. 115–153). Moscow: KomKniga/URSS.

Korotayev, A., Grinin, L. 2012. Global Urbanization and Political Development of the World System. In Grinin, L. E., Ilyin, I. V., and Korotayev, A. V. (eds.), Globalistics and Globalization Studies (pp. 28–78). Volgograd: ‘Uchitel’ Publishing House.

Korotayev, A., Grinin, L. 2013. Urbanization and Political Development of the World System. ENTELEQUIA, revista interdisciplinar 15: 197–254.

Korotayev, A., Khaltourina, D. 2006. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends in Africa. Moscow: KomKniga/URSS.

Korotayev, A., Komarova, N., Khaltourina, D. 2007. Laws of History. Secular Cycles and Millennial Trends. Demography. Economy. Wars. Moscow: Komkniga/URSS. Original in Russian (Коротаев А. В., Комарова Н. Л., Халтурина Д. А. Законы истории. Вековые циклы и тысячелетние тренды. Демография. Экономика. Войны. М.: КомКнига/URSS).

Korotayev, A., Malkov, A. 2016. A Compact Mathematical Model of the World System Economic and Demographic Growth, 1 CE – 1973 CE. International Journal of Mathematical Models and Methods in Applied Sciences 10: 200–209.

Korotayev, A., Malkov, A., Khaltourina, D. 2005. Laws of History: Mathematical Modeling of Historical Macroprocesses. Demography, Economy, Wars. Moscow: URSS. Original in Russian (Коротаев А. В., Малков А. С., Халтурина Д. А. Законы истории: Математическое моделирование исторических макропроцессов. Демография, экономика, войны. М.: КомКнига/URSS).

Korotayev, A., Malkov, A., Khaltourina, D. 2006a. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: KomKniga/URSS.

Korotayev, A., Malkov, A., and Khaltourina, D. 2006b. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends. Moscow: KomKniga/URSS.

Korotayev, A., Malkov, A. S., Khaltourina, D. A. 2007. Laws of History. Mathematical Modeling of Development of the World System. Demography. Economy. Culture. Moscow: Komkniga/URSS. Original in Russian (Коротаев А. В., Малков А. С., Халтурина Д. А. Законы истории: Математическое моделирование развития Мир-Системы. Демогра-фия, экономика, культура. М.: КомКнига/URSS).

Korotayev, A., Malkov, S. 2012. Mathematical Models of the World-System Development. In Babones, S., and Chase-Dunn, C. (eds.), Routledge Handbook of World-Systems Analysis (pp. 158–161). London: Routledge.

Korotayev, A., Zinkina, J. 2017. Systemic Boundary Issues in the Light of Mathematical Modeling of World-System Evolution. Journal of Globalization Studies 8 (1): 78–96.

Kremer, M. 1993. Population Growth and Technological Change: One Million B.C. to 1990. The Quarterly Journal of Economics 108: 681–716.

Mahdi, M. 1937. Ibn Khaldūn's Philosophy of History. A Study in the Philosophical Foundation of the Science of Culture. London: Allen & Unwin.

Masson, V. 1989. First Civilizations. Leningrad: Nauka. Original in Russian (Массон В. М. Первые цивилизации. Л.: Наука).

Morgan, L. H. 1877. Ancient Society; or, Researches in the Lines of Human Progress from Savagery, Through Barbarism to Civilization. New York: Holt.

Nefedov, S. 2008. Factor Analysis of the Historical Process. Moscow: Territoriya buduschego, Original in Russian (Нефедов С. А. Факторный анализ исторического процесса. М.: Территория будущего).

SIE – Soviet Historical Encyclopedia. 1966. Maroboduus. In Zhukov, E. (ed.), Soviet Historical Encyclopedia, vol. 9 (p. 123). Moscow: Sovetskaya entsiklopedia. Original in Russian (СИЭ. Маробод. Советская историческая энциклопедия 9: 123).

Taagepera, R. 1976. Crisis around 2005 A.D.? A Technology-population Interaction Model. General Systems 21: 137–138.

Taagepera, R. 1979. People, Skills, and Resources: An Interaction Model for World Population Growth. Technological Forecasting and Social Change 13: 13–30.

Taagepera, R. 1997. Expansion and Contraction Patterns of Large Polities: Context for Russia. International Studies Quarterly 41: 475–504.

Turchin, P. 2003. Historical Dynamics: Why States Rise and Fall. Princeton: Princeton University Press.

Turchin, P. 2005. War and Peace and War: Life Cycles of Imperial Nations. New York: Pi Press.

Turchin, P. 2007. Historical Dynamics. On the Way to Theoretical History. Moscow: Komkniga/URSS. Original in Russian (Турчин П. В. Историческая динамика. На пути к теоретической истории. М.: ЛКИ/URSS).

Turchin, P., Currie, T. E., Whitehouse, H., François, P., Feeney, K., Mullins, D., et al. 2018. Quantitative Historical Analysis Uncovers a Single Dimension of Complexity that Structures Global Variation in Human Social Organization. Proceedings of the National Academy of Sciences 115 (2): E144-E151.

Zinkina, J., Ilyin, I., Korotayev, A. 2017. The Early Stages of Globalization Evolution: Networks of Diffusion and Exchange of Domesticates, Technologies, and Luxury Goods. Social Evolution & History 16 (1): 69–85.

Zinkina, J., Malkov, A., Korotayev, A. 2014. A Mathematical Model of Technological, Economic, Demographic and Social Interaction between the Center and Periphery of the World System. In Mandal, K., Asheulova, N., and Kirdina, S. (eds.), Socio-Economic and Technological Innovations: Mechanisms and Institutions (pp. 135–147). New Delhi: Narosa.